Expectation-Maximization algorithm is used to estimate the underlying probability distribution of (observed) incomplete data. The term “incomplete data” in its general form implies the existence of two sample spaces. The observed data is a realization from a latent space.

Intuitive Explanation of EM

We want to maximize the posterior probability of the parameters $\Theta$ given the data $X$, marginalizing over $\mathbf{z}$:

\[\Theta^* = \underset {\Theta}{\text{argmax}} \sum_{\mathbf{z} \in \mathbb{Z}^n} p(\Theta,\mathbf{z} | X)\]
  • $X$: observed dataset
  • $\Theta$: the set of parameters, $\Theta = { \Theta_1, \dots, \Theta_K }$ where $\Theta_k ={ \theta_1, \dots, \theta_n }$
  • $n$: # of parameters of the distribution (If Gaussian, $n=2$, $\mu$ and $\sigma$.)
  • $K$: # of latent variables
  • $\mathbf{z}$: latent variables, $\mathbf{z} = { 1, \dots, K }$
Summary
  • Input: observed data $X$, # of latent variables
  • Output: parameter set $\Theta = {\Theta_1, \dots, \Theta_K }$

Calculation

The following figure represents the calculation of EM algorithm with Gaussian Mixture Model(GMM), assuming that, for example, there are three latent variables(mixture components).

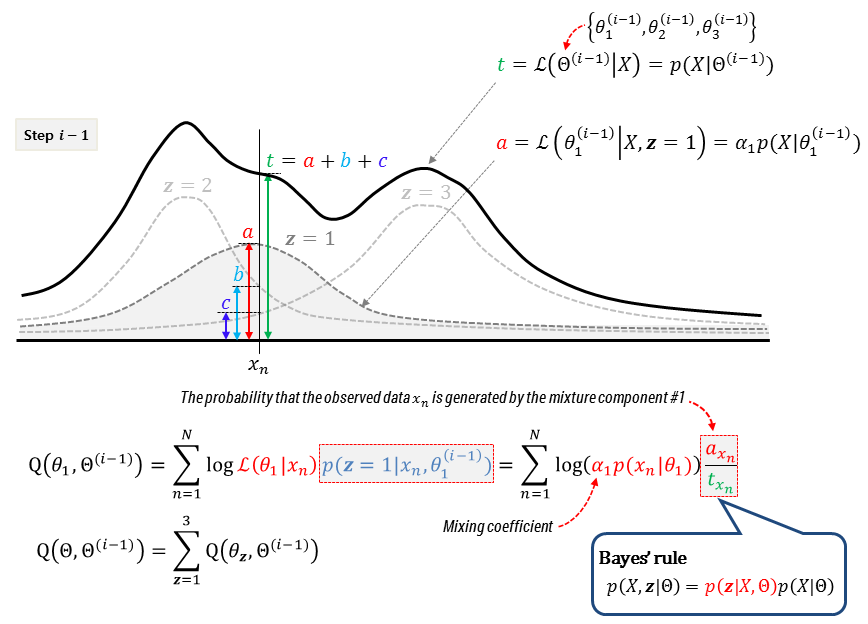
Calculation in EM procedure

References

  1. A Gentle Tutorial of the EM Algorithm and its Application to Parameter Estimation for Gaussian Mixture and Hidden Markov Models - Bilmes (1998)
  2. The Expectation Maximization Algorithm - Frank Dellaert (2002)
  3. What is the expectation maximization algorithm - Chuong B Do & Serafim Batzoglou - npg (2008)
  4. Scaling EM (Expectation-Maximization) Clustering to Large Databases - Bradley and Fayyad (1998)

See Also