Quantum Computing
고전 컴퓨터의 문제
기존의 디지털 컴퓨터는 아주 단순한 부품들로 이루어져 있고, 아주 단순한 작업을 수행한다. 컴퓨터 칩들은 모듈을 가지고 있는데, 그 모듈은 논리회로를 가지고 있고, 그 논리회로들은 트랜지스터를 포함하고 있다. 트랜지스터는 컴퓨터에서 가장 간단한 형식의 데이터 처리장치이다. 기본적으로 전기가 흐르는 통로를 막거나 여는 전기 스위치의 역할을 한다. 전기의 흐름을 열고 막음으로써 비트 상태인 0과 1을 표현하고, 여러 개의 비트 조합으로 더 복잡한 정보를 나타낼 수 있다.
오늘날의 전형적인 트랜지스터의 크기는 대략 10nm정도로 매우 작으며, 트랜지스터들이 원자 크기만큼 줄어들면, 전자들은 양자 터널링 효과라는 현상으로 인해 막혀 있는 통로(트랜지스터)를 그냥 통과할 수 있게 된다. 즉, 기술의 진보가 물리적 한계에 다다르고 있다는 것이다.
양자 컴퓨터
전자의 스핀 상태가 up(1)과 down(0)의 두 가지 상태가 가능하다고 가정하자.
Electron’s Spin
전자가 어떤 축을 중심으로 실제로 회전하는 것이 아니라, 전자 진동에 의한 어떤 물리적 특성을 가리킴.
전자가 1개라면 0, 1의 두가지 상태만 가능하지만, 전자가 2개라면 00, 01, 10, 11 의 네 가지 상태가 가능하다. 만약 전자가 $30$개라면 $2^{30}$개의 상태가 가능한 것이다.
기존의 디지털 컴퓨팅 방식에서는 계산 속도와 계산 용량을 높이기 위해 여러 개의 프로세서를 연결하여 쓰는 병렬 컴퓨팅 방식을 쓴다. 하지만 $N$개의 프로세서를 연결한 병렬 컴퓨터는 최대 $N$배 빠른 계산만 할 수 있을 뿐이다. 기껏해야 선형적으로 계산 능력이 늘어나는 방식이다.
이에 따라, 리처드 파인만(Richard Feynman)은 “양자 역학을 따르는 아주 작은 컴퓨터들”인 양자 컴퓨터로 이 문제를 해결하자는 제안을 한다.
양자 컴퓨터는 정보의 단위를 0과 1이 동시에 될 수 있는 양자 비트 (Quantum bit; Qubit; 큐빗)를 통해 큐빗 수가 늘어남에 따라 계산 공간이 지수함수적으로 늘어나는 양자 병렬성을 가진다.
큐빗의 수가 $N$개이면 중간 계산과정에서 계산공간은 $2^N$으로 커지지만, 계산의 시작과 끝은 여전히 $N$개의 비트로 나타내어 진다는 점을 잊어서는 안된다. 따라서 양자 컴퓨터의 양자 병렬성을 제대로 활용하기 위해서는 양자 알고리즘을 잘 설계해야 한다.
양자 비트 (Quantum bit; Qubit; 큐빗)
큐빗는 Dirac 표기법의 벡터 표현인 $\vert\cdot\rangle$로 표현된다:
\[\vert\psi\rangle = \alpha\vert0\rangle + \beta\vert1\rangle\]여기서 $\psi$는 파동 함수로서 큐빗의 상태를 나타낼 때 쓰고, 위 식과 같이 $\vert0\rangle$과 $\vert1\rangle$의 중첩(superposition)으로 표현할 수 있다.
여기서 $\alpha$와 $\beta$는 복소수이며, $\vert0\rangle$과 $\vert1\rangle$은 다음과 같이 표현된다:
\[\begin{aligned}\vert0\rangle = \begin{pmatrix} 1 \\ 0 \end{pmatrix}, && \vert1\rangle = \begin{pmatrix} 0 \\ 1 \end{pmatrix}\end{aligned}\]그러므로, $\vert\psi\rangle$를 다시 쓰면 다음과 같다:
\[\vert\psi\rangle = \begin{pmatrix} \alpha \\ \beta\end{pmatrix}\]양자 역학에서는, 두 개의 독립적인 양자상태(0 또는 1)가 중첩되어 있는 상태를 허용하는 two-level 시스템을 Bloch sphere를 이용하여 표현한다:

Euler Equation (Wikipedia)
\[e^{i\varphi} = \cos{\varphi} + i\sin{\varphi}\]
중첩상태에 있는 큐빗는 측정을 통해 확률적으로 $\vert0\rangle$ 또는 $\vert1\rangle$로 확정된다. 이 과정을 붕괴(collapse)한다고 말하는데, 이 때 $\vert0\rangle$를 얻을 확률은 $|\alpha|^2$이고, $\vert1\rangle$을 얻을 확률은 $|\beta|^2$로 계산된다. 이 확률들의 합은 항상 $|\alpha|^2 + |\beta|^2 = 1$이다. (Normalization)
예를 들어, 큐빗의 상태가 다음과 같은 상태에서:
\[\vert\psi\rangle = \frac{1}{\sqrt{2}}\vert0\rangle + \frac{1}{\sqrt{2}}\vert1\rangle\]측정을 했을 때, $\left |\frac{1}{\sqrt{2}} \right |^2=\frac{1}{2}$의 확률로 $\vert0\rangle$을, $\left |\frac{1}{\sqrt{2}} \right |^2=\frac{1}{2}$의 확률로 $\vert1\rangle$을 얻는다.
이러한 $\alpha$와 $\beta$를 확률진폭(probability amplitude)이라고 부른다. 즉, 중첩상태 $\vert\psi\rangle$가 $\vert0\rangle$이 될 확률진폭은 $\alpha$이고, $\vert1\rangle$이 될 확률진폭은 $\beta$인 것이다.
\[\begin{aligned} \alpha &=\cos{\frac{\theta}{2}} \\ \beta &= e^{i\phi} \sin{\frac{\theta}{2}} \end{aligned}\]Max Born’s Interpretation
슈뢰딩거의 방정식은 다음과 같다:
\[i\hbar \frac{\partial}{\partial t} \Psi(\textbf{r},t) = \left [ \frac{- \hbar^2}{2m} \nabla^2 + V(\textbf{r},t) \right ] \Psi(\textbf{r},t) = \hat{H}\vert\Psi(\textbf{r},t)\rangle\]여기서 $\textbf{r}$은 위치(position basis로 표현되는 벡터)를 나타내고, $t$는 시간을 의미한다. $\hat{H}$는 Hamiltonian 연산이다.
Max Born은 슈뢰딩거 방정식에서의 파동함수 $\Psi(\textbf{r}, t)$는 확률밀도(probability density) 함수이고, 모든 위치 $\textbf{r}$에서 적분한 결과가 1이 되는 조건:
\[\int_{-\infin}^{\infin}{\|\Psi\|^2}d\textbf{r} = 1\]를 만족하도록 파동함수 $\Psi$를 normalization 할 수 있다면, 파동함수 $\Psi$를 확률(엄밀히 말하면, 확률진폭)로 해석할 수 있다고 말했다. (이 조건에서의 $\Psi$는 normalized wave function이 된다.)
그래서, 위에서 설명한 $\alpha$와 $\beta$의 실체는 슈뢰딩거 방정식의 파동함수인 것이다.
Mathematical Backgrounds
Bra-ket Notation
- $\vert\cdot\rangle$ 표기는 켓(Ket)라고 하며, 열(column) 벡터의 형태를 가지며, 주로 양자상태를 나타낼 때 쓰인다:
\(\begin{aligned} \vert\psi\rangle = \begin{pmatrix} \psi_1 \\ \psi_2 \\ \vdots \\ \psi_N \end{pmatrix} &= \alpha_1 \begin{pmatrix} e_1 \\ 0 \\ \vdots \\ 0 \end{pmatrix} + \alpha_2 \begin{pmatrix} 0 \\ e_2 \\ \vdots \\ 0 \end{pmatrix} + \cdots + \alpha_N \begin{pmatrix} 0 \\ 0 \\ \vdots \\ e_N \end{pmatrix} \\ &= \alpha_1 \vert e_1\rangle + \alpha_2 \vert e_2\rangle + \cdots + \alpha_N \vert e_N\rangle \\ &=\sum_{n = 1}^{N} \alpha_n \vert e_n\rangle \end{aligned}\)
- 여기서 $e_n$은 eigenvalue이다.
- 양자역학에서 $\alpha_n$은 파동함수이고, $\sum_{n=1}^{N} |\alpha_n|^2 = 1$의 조건을 만족한다.
- $\langle \cdot\vert$ 표기는 브라(Bra)이라고 하며, 행(row) 벡터의 형태를 가지며, 주로 벡터를 스칼라양으로 변환하는 linear function으로 사용된다:
여기서 $x^*$는 $x$의 켤레 복소수(Complex Conjugate)를 말한다.
Complex Conjugate (Wikipedia)
켤레 복소수란 복소수의 허수부에 덧셈 역원을 취하여 얻는 복소수를 말하며, 서로 켤레인 두 복소수는 $x$축에 의하여 대칭이다.
다음 그림은 복소 평면에서 복소수 $z$와 그 켤레 복소수 $\bar{z}$(flip; 물리학에서는 $z^*$ 표기를 더 자주 사용)를 나타내고 있다:
내적 (Inner Product)
두 켓의 내적(inner product)은 다음과 같이 계산한다:
\[\begin{aligned} \langle \phi\vert\psi \rangle \coloneqq \langle \phi \vert \cdot \vert \psi \rangle &= \vert\phi\rangle^\dagger \cdot \vert\psi\rangle \\ &= \begin{pmatrix} \phi_1^* & \phi_2^* & \cdots & \phi_N^* \end{pmatrix} \begin{pmatrix} \psi_1 \\ \psi_2 \\ \vdots \\ \psi_N \end{pmatrix} \\ &= \phi_1^* \psi_1 + \phi_2^* \psi_2 + \cdots + \phi_N^* \psi_N\end{aligned}\]두 양자상태 $\vert\phi\rangle$와 $\vert\psi\rangle$의 내적$\langle \phi\vert\psi\rangle$은 일반적으로 양자상태 $\vert\psi\rangle$가 양자상태 $\vert\phi\rangle$로 붕괴(collapse)될 확률진폭으로 해석된다.
Hermitian Conjugate; Hermitian Transpose $\dagger$
$U^{\dagger}$는 $U$의 adjoint라고 하고, 행렬의 transpose 연산과 복소수의 허수부의 부호를 바꾼 complex conjugate 연산을 수행한 결과를 의미한다.
\[\begin{aligned}U &= \begin{pmatrix}1 & -2-i & 5 \\ 1+i & i & 4-2i\end{pmatrix} \\ U^T &= \begin{pmatrix}1 & 1+i \\ -2-i & i \\ 5 & 4-2i\end{pmatrix} \\ U^\dagger &= \begin{pmatrix}1 & 1-i \\ -2+i & -i \\ 5 & 4+2i\end{pmatrix}\end{aligned}\]Hermitian Conjugate Operator
\[\begin{aligned}\vert\phi\rangle &= A\vert\psi\rangle \\ &\Updownarrow \\ \vert\phi\rangle^\dagger &= \langle \phi \vert = (A\vert\psi\rangle)^\dagger = \vert\psi\rangle^\dagger A^\dagger = \langle \psi \vert A^\dagger\end{aligned}\]여기서 $N \times N$ 행렬로 나타나는 $A$는 linear operator이다.
Self-Adjoint Operator
\[A=A^\dagger\]Self-adjoint operator는 양자역학에서 매우 중요한 역할을 한다. 만약 $A$가 self-adjoint operator라면, $\langle\psi \vert A \vert \psi \rangle$는 항상 허수(complex number)가 아닌 실수(real number)이다. 이것은 관측 기대값이 실수가 될 것이라는 것을 암시한다.
외적 (Outer Product)
두 켓의 외적(outer product)은 다음과 같이 계산한다:
\[\vert\phi\rangle \langle \psi\vert = \begin{pmatrix} \phi_1 \\ \phi_2 \\ \vdots \\ \phi_N \end{pmatrix} \begin{pmatrix} \psi_1^* & \psi_2^* & \cdots & \psi_N^* \end{pmatrix} = \begin{pmatrix} \phi_1\psi_1^* & \phi_1\psi_2^* & \cdots & \phi_1\psi_N^* \\ \phi_2\psi_1^* & \phi_2\psi_2^* & \cdots & \phi_2\psi_N^* \\ \vdots & \vdots & \ddots & \vdots \\ \phi_N\psi_1^* & \phi_N\psi_2^* & \cdots & \phi_N\psi_N^* \end{pmatrix}\]외적은 크기가 $N \times N$으로, linear operator를 정의하는데 많이 이용된다.
속성 (Properties)
-
Linearity \(\begin{aligned}\langle\phi \vert \left ( c_1 \vert \psi_1\rangle + c_2 \vert \psi_2\rangle \right ) &= c_1 \langle\phi\vert\psi_1\rangle + c_2\langle\phi\vert\psi_2\rangle \\ \left ( c_1\langle\phi_1\vert + c_2\langle\phi_2\vert \right ) \vert \psi \rangle &= c_1\langle\phi_1\vert\psi\rangle + c_2\langle\phi_2\vert\psi\rangle\end{aligned}\)
- $c_1$, $c_2$는 임의의 허수(complex number)이다.
- $c^*$는 $c$의 complex conjugate이다.
- $A$는 임의의 linear operator이다.
-
Association \(\begin{aligned} \langle\psi\vert(A\vert\phi\rangle) = (\langle\psi\vertA)\vert\phi &\coloneqq \langle\psi\vertA\vert\phi\rangle \\ (A\vert\psi\rangle)\langle\phi\vert = A(\vert\psi\rangle\langle\phi\vert) &\coloneqq A\vert\psi\rangle\langle\phi\vert \end{aligned}\)
-
Hermitian Conjugation \(\begin{aligned} \langle\psi\vert^\dagger &= \vert\psi\rangle \\ (a + bi)^\dagger &= a-bi \\ (\vert\psi\rangle^\dagger)^\dagger &= \vert\psi\rangle \\ \\ (c_1\vert\psi_1\rangle + c_2\vert\psi_2\rangle)^\dagger &= c_1^* \langle \psi_1 \vert + c_2^* \langle\psi_2 \vert \\ \langle\phi \vert \psi\rangle^* &= \langle\psi \vert \phi\rangle \\ \langle\phi \vert A \vert \psi \rangle^* &= \langle\psi \vertA^\dagger \vert \phi\rangle \\ \langle\phi \vert A^\dagger B^\dagger \vert \psi \rangle^* &= \langle\psi \vert BA \vert \phi\rangle \\ ((c_1 \vert \phi_1\rangle\langle\psi_1 \vert) + (c_2 \vert \phi_2\rangle\langle\psi_2 \vert))^\dagger &= (c_1^* \vert \psi_1\rangle\langle\phi_1 \vert) + (c_2^* \vert \psi_2\rangle\langle\phi_2 \vert) \end{aligned}\)
텐서 곱 (Tensor Product)
지금까지의 설명에 언급되었던 양자 상태 $\psi$와 $\phi$는 동일한 Hilbert space $\mathcal{H}$에 존재했다.
Hilbert Space
Complete inner product space으로 정의되는 Hilbert space는 모든 코시 수열(Cauchy sequence)의 극한이 존재하는 내적 공간(inner product space)이다.
Inner Product Space
Inner product라는 추가적인 수학적 구조를 가진 벡터 공간이다. 여기서 말하는 inner product structure는 이 공간에 존재하는 벡터 쌍과 벡터들 간의 내적(inner product)으로 알려진 스칼라양이 연관되어 있는 구조를 말한다.
Cauchy Sequence
수열이 진행됨에 따라 각 요소들이 서로 점점 가까워져 수렴하는 수열을 코시 수열이라고 한다. 다음 그림에서 첫번째는 코시 수열이지만, 두번째는 코시 수열이 아니다.

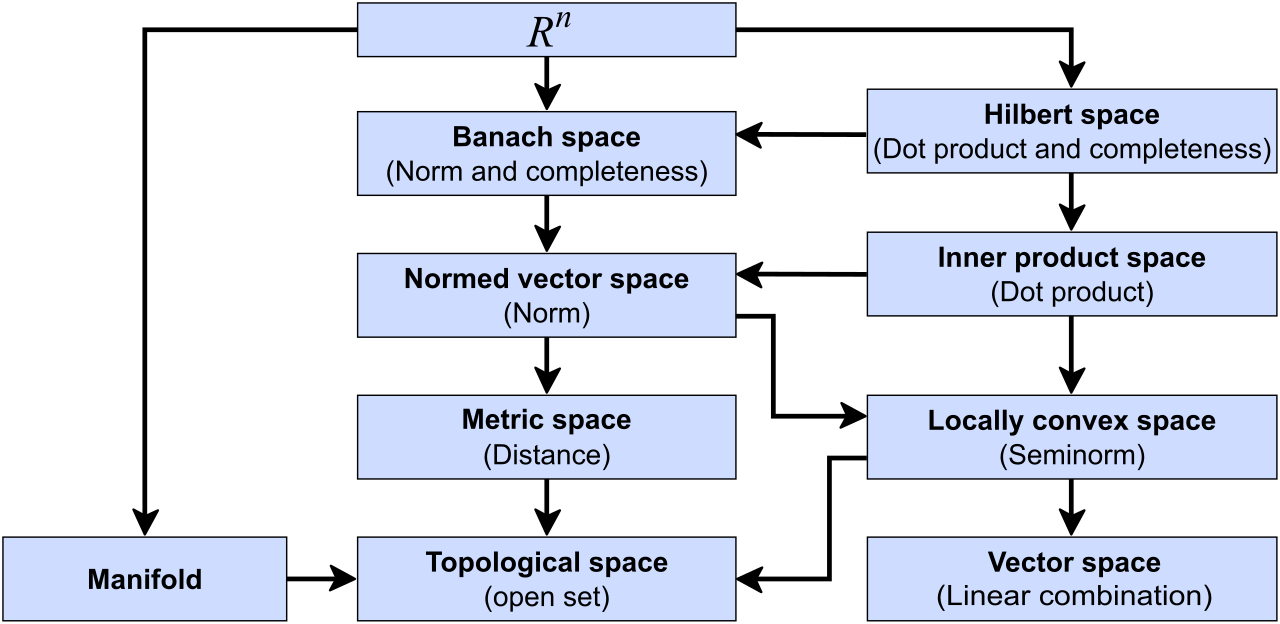
Overview of Types of Abstract Spaces
Space $A \rightarrow B$는 generalization으로, space $A$가 space $B$의 한 종류이기도 하다라는 것을 의미한다. 즉, “모든 Hilbert space는 Banach space이다”라는 말은 참(true)이다. 하지만 어떤 Banach space는 Hilbert space가 아닐 수 있다.
그런데, 서로 다른 Hilbert space $\mathcal{H}_1^N$과 $\mathcal{H}_2^M$는 텐서 곱(tensor product) 연산으로 제 3의 새로운 space $(\mathcal{H}_1 \otimes \mathcal{H}_2)^{N \times M}$를 형성할 수 있는데, 서로 다른 Hilbert space 존재하는 두 켓 $\vert\psi\rangle \in \mathcal{H}_1$, $\vert\phi\rangle \in \mathcal{H}_2$의 direct product 연산은 다음과 같이 표현하고,
\[\begin{aligned}\vert\psi\rangle \vert\phi\rangle &\in \mathcal{H}_1\otimes\mathcal{H}_2 \\ &\text{or} \\ \vert\psi\rangle\otimes \vert\phi\rangle &\in \mathcal{H}_1\otimes\mathcal{H}_2 \\ &\text{or} \\ \vert\psi\phi\rangle &\in \mathcal{H}_1\otimes\mathcal{H}_2 \\ &\text{or} \\ \vert\psi,\phi\rangle &\in \mathcal{H}_1\otimes\mathcal{H}_2 \end{aligned}\]연산 결과도 켓($N\times M$)으로 나타난다. 두 켓의 텐서 곱은 다음과 같이 계산한다:
\[\begin{aligned} \vert\psi\rangle \otimes \vert\phi\rangle &= \begin{pmatrix} \psi_1 \\ \psi_2 \\ \vdots \\ \psi_N \end{pmatrix} \otimes \begin{pmatrix} \phi_1 \\ \phi_2 \\ \vdots \\ \phi_M \end{pmatrix} \\ &= \begin{pmatrix} \psi_1\phi_1 & \psi_1\phi_2 & \cdots & \psi_1\phi_M \\ \psi_2\phi_1 & \psi_2\phi_2 & \cdots & \psi_2\phi_M \\ \vdots & \vdots & \ddots & \vdots \\ \psi_N\phi_1 & \psi_N\phi_2 & \cdots & \psi_N\phi_M \end{pmatrix} \end{aligned}\] \[\begin{aligned}(1 \leq n \leq N, && 1 \leq m \leq M)\end{aligned}\](이 공간에서 켓은 위와 같이 $N\times M$ 행렬로 표현되고, 브라는 $M\times N$ 행렬로 표현된다.)
만약 여기서 측정(measurement)이 일어난다면, $\vert\psi\rangle$는 $\mathcal{H}_1$ 공간에서 $\vert\psi_n\rangle$으로, $\vert\phi\rangle$은 $\mathcal{H}_2$ 공간에서 $\vert\phi_m\rangle$으로 붕괴(collapse)될 것이므로, $\mathcal{H}_1\otimes\mathcal{H}_2$ 공간에서는 $N \times M$개의 쌍(pair) 중 하나인 $\vert\psi_n\rangle\otimes \vert\phi_m\rangle$으로 붕되될 것이다.
References
- https://en.wikipedia.org/wiki/Tensor_product
- https://en.wikipedia.org/wiki/Hilbert_space
- https://physics.stackexchange.com/questions/54896/should-it-be-obvious-that-independent-quantum-states-are-composed-by-taking-the
- https://physics.stackexchange.com/questions/134575/tensor-product-of-a-bra-and-a-ket
브라와 켓의 텐서 곱은 다음과 같이 계산한다:
\[\begin{aligned} \vert A\rangle \otimes \langle B\vert \coloneqq \vert A\rangle \otimes \vert B\rangle^\dagger &= \begin{pmatrix} a_1 \\ a_2 \\ a_3 \\ a_4 \end{pmatrix} \otimes \begin{pmatrix} b_1 & b_2 & b_3 & b_4 \end{pmatrix} \\ &= \begin{pmatrix} a_1b_1 & a_1b_2 & a_1b_3 & a_1b_4 \\ a_2b_1 & a_2b_2 & a_2b_3 & a_2b_4 \\ a_3b_1 & a_3b_2 & a_3b_3 & a_3b_4 \\ a_4b_1 & a_4b_2 & a_4b_3 & a_4b_4 \end{pmatrix} \end{aligned}\]텐서 (Tensor)
어떻게 바라보아도 그 본질이 변하지 않는 것을 텐서라고 한다. 이것을 수학적으로 정의하면, 어떠한 좌표변환을 하더라도 변하지 않는 것을 텐서라고 한다.
그럼 예를 들어, 중력은 텐서일까? 중력은 텐서가 아니다. 만약 중력이 텐서라면 중력에 의해 영향을 받는 모든 공간에서 중력을 느낄 수 있어야 한다. 하지만 자유낙하하는 공간(예를 들면, 줄이 끊어져 자유낙하하는 엘리베이터 내부)에서는 중력을 느낄 수가 없다. 자유낙하 중에는 아무리 무거운 물체를 들어올려도 무게를 느낄 수 없으며, 내 자신의 몸무게도 사라진다.
또 다른 예로, 위치를 나타내는 벡터는 텐서가 아니다. 보통 벡터는 rank가 1인 텐서라고 말하는데, 위치벡터는 텐서가 아니다. 위치라는 것은 기준이 되는 원점이 있어야 정의가 되기 때문에, 전 우주에서 절대적인 원점은 존재하지 않으며, 위치벡터를 정의하는 기준점이 바뀌면 위치벡터는 변하게 되기 때문에 위치벡터는 텐서가 아니다. 즉, 위치벡터의 기준이 되는 원점은 사람이 수학계산을 편하게 하기 위해 기준을 설정한 것일 뿐 그 기준은 언제든 변할 수 있고, 위치벡터는 어느 좌표계에서든 불변하는 것이 아니기 때문에 텐서가 될 수 없다.
하지만, 두 위치 벡터의 차이는 텐서이다. 왜냐하면 좌표계와 상관 없이 정의될 수 있는 물리량이기 때문이다.
두 큐빗로 이루어진 시스템 (2-Qubits System)
이 시스템은 네 가지의 상태 $\vert 00\rangle$, $\vert 01\rangle$, $\vert 10\rangle$, $\vert 11\rangle$를 가진다. 역시 중첩으로 표현 가능하며, 큐빗는 다음과 같이 표현된다:
\[\vert 00\rangle = \begin{pmatrix} 1 \\ 0 \\ 0 \\ 0 \end{pmatrix}, \vert 01\rangle = \begin{pmatrix} 0 \\ 1 \\ 0 \\ 0 \end{pmatrix}, \vert 10\rangle = \begin{pmatrix} 0 \\ 0 \\ 1 \\ 0 \end{pmatrix}, \vert 11\rangle = \begin{pmatrix} 0 \\ 0 \\ 0 \\ 1 \end{pmatrix}\] \[\vert\psi\rangle = \alpha_{00}\vert 00\rangle + \alpha_{01}\vert 01\rangle + \alpha_{10}\vert 10\rangle + \alpha_{11}\vert 11\rangle\]역시 마찬가지로, $\alpha_{00}$, $\alpha_{01}$, $\alpha_{10}$, $\alpha_{11}$은 복소수이며, coefficient 또는 amplitude라고 부른다. 또한, $\vert 00\rangle$이 나타날 확률은 $|\alpha_{00}|^2$이고, $|\alpha_{00}|^2 + |\alpha_{01}|^2 + |\alpha_{10}|^2 + |\alpha_{11}|^2 = 1$이다:
\[\sum_{x \in { \left \{ 0,1 \right \} }^2} |\alpha_x|^2 = 1\]특별히, 2-Qubits system의 큐빗가 다음과 같은 상태일 때 Bell state라고 부른다:
\[\vert\psi\rangle = \frac{1}{\sqrt{2}}\vert 00\rangle + \frac{1}{\sqrt{2}}\vert 11\rangle\]이 경우, 첫 번째 큐빗를 측정하면 50%의 확률로 각각 $\vert 0\rangle$과 $\vert 1\rangle$을 얻을 수 있다. 그런데 측정 후 $\vert 0\rangle$을 얻은 후 두 번째 큐빗는 항상 $\vert 0\rangle$을 얻게 된다. 반대로, 두 번째 큐빗를 먼저 측정 하고 첫 번째 큐빗를 측정해도 이와 동일한 현상이 발생한다. 이 성질을 얽힘 현상(Entanglement)이라고 한다.
아래와 같은 경우는 또 다른 상황을 나타낸다:
\[\vert\psi\rangle = \frac{1}{\sqrt{2}}\vert 00\rangle + \frac{1}{\sqrt{2}}\vert 01\rangle\]첫 번째 큐빗를 측정한 Alice는 $\vert 0\rangle$을 100%의 확률로 측정하게 된다. 두 번째 큐빗를 Bob이 측정하면 50%의 확률로 $\vert 0\rangle$과 $\vert 1\rangle$이 측정된다. 위 식은 아래와 같이 분리될 수 있는데,
\[\vert\psi\rangle = \frac{1}{\sqrt{2}}\vert 00\rangle + \frac{1}{\sqrt{2}}\vert 01\rangle = \vert 0\rangle \otimes \left (\frac{1}{\sqrt{2}}\vert 0\rangle + \frac{1}{\sqrt{2}}\vert 1\rangle \right )\]이는 첫 번재 큐빗 $\vert 0\rangle$은 Alice가, 두 번째 큐빗는 $\frac{1}{\sqrt{2}}\vert 0\rangle + \frac{1}{\sqrt{2}}\vert 1\rangle$의 상태에서 측정하기 때문에 얽힘 현상은 발생하지 않는다. 이를 분리가능(separable)이라고 한다. ($\otimes$는 텐서곱이라고 한다.)
2-Qubits System은 $n$-Qubits System으로 확장시킬 수 있는데, computational basis state는 $\vert x_1, x_2, x_3, \cdots, x_n \rangle$이고, 동시에 $2^n$개의 상태를 표현할 수 있다.
단일 큐빗 양자 게이트 (Single Qubit Quantum Gate)
고전 컴퓨터에는 여러 가지 논리 게이트가 존재한다: NOT, AND, OR, XOR 등… 이와 유사하게, 양자 컴퓨터에는 양자 게이트가 있다.
Pauli-X Gate ($\textbf{NOT}$ Gate)
NOT 게이트는 큐빗를 다음과 같이 바꿔 준다(bit-flip):
\[\vert 0\rangle \rightarrow \vert 1\rangle\]하지만 큐빗는 $\alpha\vert 0\rangle + \beta\vert 1\rangle$의 상태로 존재하기 때문에 NOT 게이트를 적용하면,
\[\alpha\vert 0\rangle + \beta\vert 1\rangle \rightarrow \alpha\vert 1\rangle + \beta\vert 0\rangle\]로 바뀐다(Linear operation). 이러한 NOT 양자 게이트 $X$는 행렬로 표현할 수 있다:
\[\textbf{NOT} = X \equiv \begin{pmatrix} 0 & 1 \\ 1 & 0 \end{pmatrix}\]단일 큐빗도 행렬로 표현하면 다음과 같이 표현할 수 있고,
\[\vert\psi\rangle = \alpha\vert 0\rangle + \beta\vert 1\rangle \Rightarrow \alpha\begin{pmatrix} 1 \\ 0 \end{pmatrix} + \beta\begin{pmatrix} 0 \\ 1 \end{pmatrix} = \begin{pmatrix} \alpha \\ \beta \end{pmatrix}\]NOT 게이트 연산도 행렬 연산으로 나타낼 수 있다:
\[\begin{aligned} X\vert\psi\rangle = X\begin{pmatrix} \alpha \\ \beta \end{pmatrix} &= \begin{pmatrix} 0 & 1 \\ 1 & 0 \end{pmatrix} \begin{pmatrix} \alpha \\ \beta \end{pmatrix} \\ &= \begin{pmatrix} \beta \\ \alpha \end{pmatrix} \\ &= \beta\begin{pmatrix} 1 \\ 0 \end{pmatrix} + \alpha\begin{pmatrix} 0 \\ 1 \end{pmatrix} \\ &= \beta\vert 0\rangle + \alpha\vert 1\rangle \end{aligned}\]양자 상태는 normalization condition을 만족하는데, $\alpha\vert 0\rangle + \beta\vert 1\rangle$에서 $|\alpha|^2 + |\beta|^2 = 1$이고, 양자 게이트 연산 후 바뀐 상태 $\vert\psi^\prime\rangle = \alpha^\prime\vert 0\rangle + \beta^\prime\vert 1\rangle$ 역시 $\vert\alpha^\prime|^2 + |\beta^\prime|^2 = 1$을 만족한다.
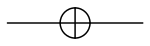
$X$ 게이트의 퀀텀 회로 다이어그램은 다음과 같이 나타낸다:
Unitary
양자 게이트가 되기 위해서는 unitary여야 한다. Unitary는 다음의 성질을 만족해야 한다:
\[U^{\dagger}U = I\]
Pauli-Y Gate
\[Y \equiv \begin{pmatrix} 0 & -i \\ i & 0 \end{pmatrix}\]$Y$ 게이트는 Bloch sphere의 $y$축 기준으로 $\pi$ 만큼 회전하는 변환을 수행한다:
\[\begin{aligned} Y\vert\psi\rangle = Y\begin{pmatrix} \alpha \\ \beta \end{pmatrix} &= \begin{pmatrix} 0 & -i \\ i & 0 \end{pmatrix} \begin{pmatrix} \alpha \\ \beta \end{pmatrix} \\ &= \begin{pmatrix} -\beta i \\ \alpha i \end{pmatrix} \\ &= -\beta i \begin{pmatrix} 1 \\ 0 \end{pmatrix} + \alpha i \begin{pmatrix} 0 \\ 1 \end{pmatrix} \\ &= -\beta i \vert 0\rangle + \alpha i \vert 1\rangle \end{aligned}\]Pauli-X Gate 연산과의 비교
$Y$ 게이트는 Bloch sphere에서 $y$축을 기준으로 $\pi$만큼 회전한다면, $X$ 게이트는 $x$축을 기준으로 $\pi$만큼 회전한다고 볼 수 있다. 같은 방식으로, 바로 뒤에서 설명할 $Z$ 게이트는 $z$축을 기준으로 $\pi$만큼 회전하는 변환을 수행한다.
Pauli-Z ($R_\pi$) Gate
\[Z \equiv \begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix}\]$Z$ 게이트는 다음과 같이 phase-flip 연산을 수행한다:
\[\begin{aligned} Z\vert\psi\rangle = Z\begin{pmatrix} \alpha \\ \beta \end{pmatrix} &= \begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix} \begin{pmatrix} \alpha \\ \beta \end{pmatrix} \\ &= \begin{pmatrix} \alpha \\ -\beta \end{pmatrix} \\ &= \alpha\begin{pmatrix} 1 \\ 0 \end{pmatrix} - \beta\begin{pmatrix} 0 \\ 1 \end{pmatrix} \\ &= \alpha\vert 0\rangle - \beta\vert 1\rangle \end{aligned}\]연산 결과를 좀 더 살펴보자면, $Z$ 게이트 연산 후 $\vert 0\rangle$은 변화 없고, $\beta\vert 1\rangle$만 $-\beta\vert 1\rangle$로 변한 것을 알 수 있다.
$Z^\dagger Z = I$도 성립한다.
Phase Shift Gate
\[R_\phi \equiv \begin{pmatrix} 1 & 0 \\ 0 & e^{i\phi} \end{pmatrix}\]$Z$ 게이트는 Bloch sphere에서 $z$축을 기준으로 $\pi$만큼 회전하는 연산을 수행한다면, Phase Shift Gate는 $\phi$(phase shift)만큼 회전하는 연산을 수행한다. 다시 말해서, $Z$ 게이트는 $\phi=\pi$인 phase shift 게이트이다. 또한, $\phi = \frac{\pi}{4}$인 phase shift 게이트를 $T$ 게이트라고 하고, $\phi = \frac{\pi}{2}$인 phase shift 게이트를 $S$ 게이트라고 한다.
Square-Root of NOT Gate ($\sqrt{\textbf{NOT}}$)
\[\sqrt{X} = \sqrt{\textbf{NOT}} = \sqrt{\neg} \equiv \frac{1}{2} \begin{pmatrix} 1+i & 1-i \\ 1-i & 1+i \end{pmatrix}\]
이 게이트의 연산을 통한 큐빗의 상태는 다음과 같이 달라진다:
\[\begin{aligned} \sqrt{\neg}\vert\psi\rangle = \sqrt{\neg}\begin{pmatrix} \alpha \\ \beta \end{pmatrix} &= \frac{1}{2} \begin{pmatrix} 1+i & 1-i \\ 1-i & 1+i \end{pmatrix} \begin{pmatrix} \alpha \\ \beta \end{pmatrix} \\ &= \begin{pmatrix} \frac{(1+i)\alpha+(1-i)\beta}{2} \\ \frac{(1-i)\alpha+(1+i)\beta}{2} \end{pmatrix} \\ &= \frac{(1+i)\alpha+(1-i)\beta}{2} \begin{pmatrix} 1 \\ 0 \end{pmatrix} + \frac{(1-i)\alpha+(1+i)\beta}{2} \begin{pmatrix} 0 \\ 1 \end{pmatrix} \\ &= \frac{(1+i)\alpha+(1-i)\beta}{2} \vert 0\rangle + \frac{(1-i)\alpha+(1+i)\beta}{2} \vert 1\rangle \end{aligned}\]Hadamard($H$) Gate
$H$ 게이트는 아주 중요한 양자 게이트 중 하나로 $\vert 0\rangle$을 $\frac{\vert 0\rangle + \vert 1\rangle}{\sqrt{2}}$로, $\vert 1\rangle$을 $\frac{\vert 0\rangle - \vert 1\rangle}{\sqrt{2}}$로 매핑시키며, 측정행위가 동일한 확률로 1 또는 0으로 확정되는 중첩상태(Superposition)를 만들 수 있다. (참고로, $H$ 게이트는 양자 푸리에 변환(Quantum Fourier Transform)의 단일 큐빗 버전이다.)
\[H \equiv \frac{1}{\sqrt{2}}\begin{pmatrix} 1 & 1 \\ 1 & -1 \end{pmatrix}\]
$H$ 게이트는 $X$ 게이트와 $Z$ 게이트의 조합으로 표현될 수 있다:
\[H=\frac{X+Z}{\sqrt{2}}\] \[\begin{aligned} H\vert\psi\rangle = H\begin{pmatrix} \alpha \\ \beta \end{pmatrix} &= \frac{1}{\sqrt{2}}X\begin{pmatrix} \alpha \\ \beta \end{pmatrix} + \frac{1}{\sqrt{2}}Z\begin{pmatrix} \alpha \\ \beta \end{pmatrix} \\&= \frac{1}{\sqrt{2}}\begin{pmatrix} 0 & 1 \\ 1 & 0 \end{pmatrix}\begin{pmatrix} \alpha \\ \beta \end{pmatrix} + \frac{1}{\sqrt{2}}\begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix}\begin{pmatrix} \alpha \\ \beta \end{pmatrix} \\&= \frac{\beta}{\sqrt{2}}\vert 0\rangle + \frac{\alpha}{\sqrt{2}}\vert 1\rangle + \frac{\alpha}{\sqrt{2}}\vert 0\rangle - \frac{\beta}{\sqrt{2}}\vert 1\rangle \\ &= \frac{\alpha+\beta}{\sqrt{2}}\vert 0\rangle + \frac{\alpha-\beta}{\sqrt{2}}\vert 1\rangle \end{aligned}\]$H$ 게이트 역시 $H^\dagger H = I$가 성립한다.
다수의 큐빗 양자 게이트 (Multiple Qubit Quantum Gate)
SWAP Gate
\[\textbf{SWAP} \equiv \begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix}\]
SWAP 게이트의 연산은 다음과 같다:
\[\vert\psi\rangle = \alpha_{00}\vert 00\rangle + \alpha_{01}\vert 01\rangle + \alpha_{10}\vert 10\rangle + \alpha_{11}\vert 11\rangle = \begin{pmatrix} \alpha_{00} \\ \alpha_{01} \\ \alpha_{10} \\ \alpha_{11} \end{pmatrix}\] \[\begin{aligned} \textbf{SWAP}\vert\psi\rangle &= \begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} \alpha_{00} \\ \alpha_{01} \\ \alpha_{10} \\ \alpha_{11} \end{pmatrix} = \begin{pmatrix} \alpha_{00} \\ \alpha_{10} \\ \alpha_{01} \\ \alpha_{11} \end{pmatrix} \\ &= \alpha_{00}\vert 00\rangle + \alpha_{10}\vert 01\rangle + \alpha_{01}\vert 10\rangle + \alpha_{11}\vert 11\rangle \end{aligned}\]Controlled Gate ($cX$, $cY$, $cZ$ Gate)
Controlled Gate는 2개 이상의 큐빗을 input으로 가진다. 예를 들어, Controlled-NOT(CNOT, $cX$) 게이트가 있는데:
\[\textbf{CNOT} = cX \equiv \begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0 \end{pmatrix}\]
이 게이트는 입력이 두 개이다. 하나는 control 큐빗, 다른 하나는 target 큐빗이다. 첫번째 큐빗이 $\vert 1\rangle$일 때만 두번째 큐빗에 대해서 $\textbf{NOT}$ 연산을 수행한다:
\[\begin{aligned} \vert 00\rangle &\mapsto \vert 00\rangle \\ \vert 01\rangle &\mapsto \vert 01\rangle \\ \vert 10\rangle &\mapsto \vert 1\rangle \otimes X\vert 0\rangle = \vert 1\rangle \otimes \begin{pmatrix} 0 & 1 \\ 1 & 0 \end{pmatrix}\begin{pmatrix} 1 \\ 0 \end{pmatrix} = \vert 1\rangle \otimes \begin{pmatrix} 0 \\ 1 \end{pmatrix} = \vert 1\rangle \otimes \vert 1\rangle = \vert 11\rangle \\ \vert 11\rangle &\mapsto \vert 1\rangle \otimes X\vert 1\rangle = \vert 1\rangle \otimes \begin{pmatrix} 0 & 1 \\ 1 & 0 \end{pmatrix}\begin{pmatrix} 0 \\ 1 \end{pmatrix} = \vert 1\rangle \otimes \begin{pmatrix} 1 \\ 0 \end{pmatrix} = \vert 1\rangle \otimes \vert 0\rangle = \vert 10\rangle \end{aligned}\]그리고, CNOT 게이트와 단일 큐빗 양자 게이트의 조합으로 다른 모든 양자 연산을 수행할 수 있다.
$cX$, $cY$, $cZ$ 게이트의 도식은 각각 다음과 같다:
\[\begin{matrix}cX \equiv \begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0 \end{pmatrix} & cY \equiv \begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & -i \\ 0 & 0 & i & 0 \end{pmatrix} & cZ \equiv \begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & -1 \end{pmatrix}\end{matrix}\]


TODO:
측정 (Measurement)

왼쪽의 한줄은 qubit을 나타내고, 오른쪽의 두줄은 classical bit를 나타낸다.
측정은 비가역적이기 때문에 양자 게이트가 아니다. 측정 행위는 관측 대상인 큐빗을 한가지의 값으로 할당한다. (Collapse) 다시 말해서, 여러 개의 큐빗으로 구성되는 양자 상태가 측정을 통해 하나의 base vector로 결정된다.
양자 컴퓨터의 구현
기존의 디지털 컴퓨터는 주로 반도체 실리콘을 바탕으로 만들어졌지만, 양자 컴퓨터는 어떤 방식으로 구현될지 아직은 다양한 제안들 속에서 모색 중이다.
양자 컴퓨터를 구현하기 위한 다섯 가지 요건은 다음과 같다:
- 분명히 구별 가능한 두 상태 (0과 1)를 가진 양자계로서 확장 가능해야 한다. (Scalability)
- 기준이 되는 (예를 들면, 0) 양자 상태를 만들 수 있어야 한다.
- 필요한 양자 연산 게이트들을 구현할 수 있어야 한다.
- 단일 큐빗는 비교적 쉽게 구현하지만, 얽힘(Entanglement) 상태를 구현해야만 독립된 두 개의 큐빗를 쌍으로 만들어 00, 01, 10, 11을 표현할 수 있는데, 이 얽힘 상태를 구현하는 것이 정말 쉽지 않다. 현재 학계에서는 이온덫(Ion Trap) 방법이 가장 유리할 것으로 기대하고 있고, 업계에서는 초전도체 및 반도체 나노 소자를 이용한 양자 게이트 개발을 시도하고 있다.
- 연산 과정에서 외부와의 상호작용을 완벽히 차단할 수 있어야 한다. (Coherence)
- 양자 계산 완료 후 최종 상태에 이르렀을 때 원하는 정보를 측정할 수 있어야 한다.
스핀트로닉스
양자 컴퓨터의 구현에 있어 가장 어려운 점의 핵심은 큐빗(Qubit)를 제대로 제어하기 어렵다는 데 있다. 제어가 가장 용이할 것으로 예측되는 전자의 스핀조차 실용적인 수준의 컴퓨팅을 구현하기에는 일정한 상태를 유지할 수 있는 시간이 너무 짧다. 즉, 정보의 안정성이 보장되지 않는 것이다.
그래서 전자의 스핀을 제어하는 방법에 연구가 활발히 진행되고, 이러한 연구는 스핀트로닉스라는 명칭을 얻게 되었다.
References
- 10년 후의 반도체 물리학 - 양자컴퓨터.pdf
- [번역] 고양이, 큐비트, 그리고 순간이동 - 양자 연산 애플리케이션의 이상한 세계(3편)
- 양자 원리와 컴퓨터 - 양자컴퓨터.pdf
- 말 많은 양자컴퓨터, 오해와 사실 - IBS