Introduction

베이지안 접근방식에서 가장 어려운 점은 추론 과정에서 다차원의 함수에 대해 integration을 요한다는 것이다. 여기서 소개할 MCMC(Markov chain Monte Carlo) method는 우리의 관심의 대상이 되는 (복잡한) target distribution(예를 들어, 앞에서 말한 posterior distribution)으로부터 표본을 채취(sampling)하여 그 (target) distribution을 simulation하는 방법이다.

Monte Carlo Integration

MCMC에 대해 살펴보기 전에 먼저 Monte Carlo method (줄여서 MC method)에 대해 알아보자. 본래 MC method은 난수를 생성하여 적분을 계산하기 위한 방법이었다.

예를 들어, 아래 그림과 같이 $\pi$의 값을 맞추기 위해 난수를 발생시키고 파란색의 점과 빨간색의 점의 갯수를 세서 $\pi$의 값을 알아내는 방식이 Monte Carlo method이다. 그리고, 생성된 난수의 개수가 많을수록 더욱 정확하게 $\pi=3.141592\cdots$를 근사하는 것을 알 수 있다.

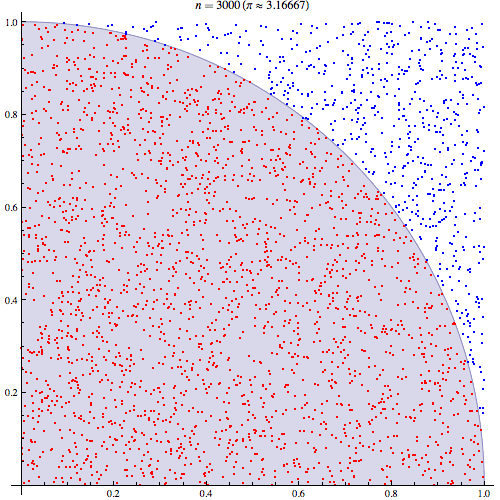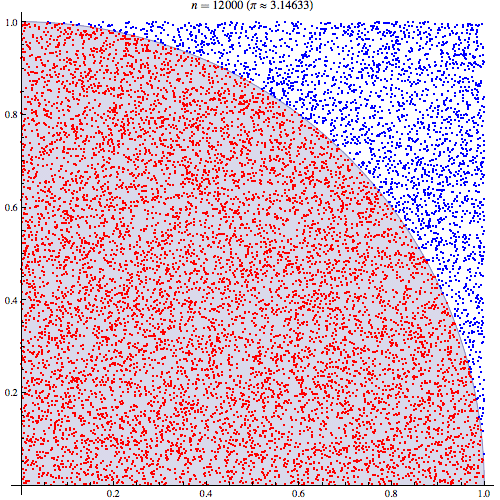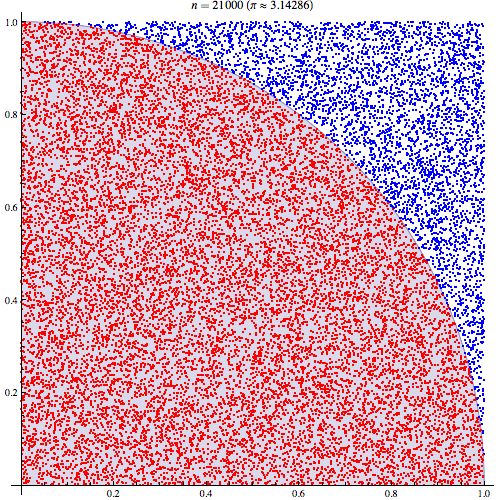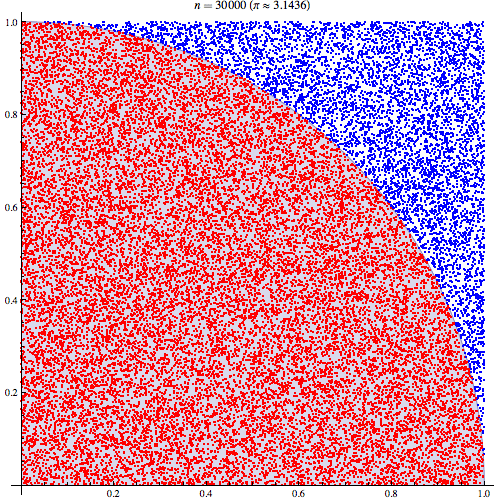
monte carlo integration

이제 좀 더 자세히 베이지안 통계학에서 Monte Carlo method가 어떻게 수행되는지 살펴보자. 우리의 관심의 대상이 되는 값 $\theta$가 다음과 같을 때,

\[\theta = \int_a^b h(x)dx\]

$h(x)$를 임의의 함수 $f(x)$와 $(a,b)$구간에서 정의된 어느 특정 확률분포 $p(x)$의 곱으로 표현할 수 있다면 다음과 같이 쓸 수 있다:

\[\theta = \int_a^b h(x)dx = \int_a^b f(x)p(x)dx = E_p \left [ f(x) \right ]\]

결국, integral은 $x$에 관한 특정 함수 $f(x)$에 대한 기대값(expectation)으로 나타낼 수 있다. 이것을 Monte Carlo integration이라고 부른다. 뒤에서 다루겠지만, 이 Monte Carlo method는 베이지안 통계학에서 posterior distribution을 근사하여 parameter를 estimation하는 데에 사용될 수 있다.

Importance Sampling

Suppose that a distribution $q(x)$ is used to approximate the target distribution $p(x)$. Then we can describe as:

\[\int f(x)p(x)dx = \int f(x) \left ( \frac{p(x)}{q(x)} \right ) q(x)dx = E_q \left [ f(x) \left ( \frac{p(x)}{q(x)} \right ) \right ]\]

This form is called the importance sampling and we can say that

\[\int f(x)p(x)dx \simeq \frac{1}{M} \sum_{i=1}^M f(x_i)\left( \frac{p(x_i)}{q(x_i)} \right)\]

where $x_i$ is a sample drawn from the distribution $q(x)$ which approximates $p(x)$.

Markov chain Monte Carlo, MCMC

임의의 분포 $p(x)$가 있다고 가정하자. (여기서 분포 $p$는 univariate 또는 multivariate이다.) 이 분포를 추정하기 위해 해당 분포로부터 직접 sampling을 수행하는 것이 앞에서 말한 Monte Carlo method이다. 하지만 해당 분포로부터 직접 random number generation이 매우 어려운 경우에는 어떻게 할까?

MCMC는 이러한 Monte Carlo method의 단점을 보완한 방법으로 해당 분포로부터 직접 random number generation 하는 대신에, stationary distribution을 가지는 Markov chain $p(x^{(i)}\vert x^{(i-1)})$을 만들어 random number generation을 수행한다. MCMC에 대해 설명하기 이전에 Markov chain에 대해 먼저 알아보자.

Markov chain

Markov chain is a sequence of random variables $x^{(0)},x^{(1)},x^{(2)},\cdots$ with the Markov property.

Markov property

The transition probability is dependent on only the current state, not on any previous states.

\[p(x^{(i)}\vert x^{(i-1)},x^{(i-2)}, \cdots, x^{(1)},x^{(0)})=p(x^{(i)}\vert x^{(i-1)})\]

만약 우리의 관심의 대상이 되는 $x$에 대해서 현재 상태의 $x^{(i)}$값이 이전 상태의 $x^{(i-1)}$값에 dependent 하고, 이에 대한 확률 $p(x^{(i)}\vert x^{(i-1)})$이 결국 수렴된다면 우리는 MCMC를 사용할 수 있다.

MCMC가 수행되는 과정은 다음과 같다:

  • Step #1: Markov chain ${ x^{(0)}, x^{(1)}, \cdots, x^{(M)} }$을 만든다. ($x^{(M)}$값은 stationary distribution을 따른다.)
  • Step #2: Step #1을 $n$번 반복한다. ($n$개의 $x^{(M)}$들이 density function $p(x)$를 따르는 random sample들이다.)

좋은 random number generation을 위해서는 step #1에서 $M$를 충분히 크게 해 주어야 하고, 이 과정은 초기값 $x^{(0)}$에 영향을 받지 않게 하는 과정으로 burn-in이라고 부른다.

Gibbs sampling

Gibbs sampling은 두 개 이상의 변수들의 joint distribution으로부터 연쇄적으로 표본을 추출하는데, 앞에서 말한 MCMC에서 target distribution을 추정할 때 매우 중요한 역할을 한다.

Gibbs sampling을 사용하려면 joint distribution으로부터 각 변수들에 대한 full conditional distribution을 모두 구해내야 한다.

Full conditional distribution
\[\begin{aligned}x_j \sim p(x_j\vert x_{-j})&=p(x_j\vert x_1, \cdots, x_{j-1}, x_{j+1}, \cdots, x_n)\\&=\frac{p(x_1, x_2, \cdots, x_n)}{p(x_1, \cdots, x_{j-1}, x_{j+1}, \cdots, x_n)}\propto p(x_1, x_2, \cdots, x_n) \end{aligned}\]

Gibbs sampling은 다음과 같이 수행된다:

  • Initialization: Set $X^{(0)} = { x_1^{(0)}, x_2^{(0)}, \cdots, x_n^{(0)} }$ as some initial values.
  • Step #1: Sample $X^{(i)}$ from the full conditional distributions.
\[X^{(i)}=\left \{ \begin{aligned}x_1^{(i)} &\sim p(x_1\vert x_2^{(i-1)}, x_3^{(i-1)}, x_4^{(i-1)}, \cdots, x_n^{(i-1)})\\x_2^{(i)} &\sim p(x_2\vert x_1^{(i)}, x_3^{(i-1)}, x_4^{(i-1)}, \cdots, x_n^{(i-1)})\\x_3^{(i)} &\sim p(x_3\vert x_1^{(i)}, x_2^{(i)}, x_4^{(i-1)}, \cdots, x_n^{(i-1)})\\&\vdots\\x_n^{(i)} &\sim p(x_n\vert x_1^{(i)}, x_2^{(i)}, x_3^{(i)}, \cdots, x_{n-1}^{(i)})\end{aligned} \right .\]
  • Step #2: Back to Step #1
\[i \leftarrow i+1\]

Gibbs sampling for $n$-dimensional distribution $p(X)$

이렇게 추출된 표본들은 모든 변수들의 joint distribution을 근사한다. 그리고, 특정 변수에 대한 기대값은 모든 표본들을 averaging함으로써 근사할 수 있다. 만약 burn-in 후 $M$개의 sample들이 생성되었다면, $M$이 커지면 커질수록 다음을 만족한다.

\[\frac{1}{M} \sum_{m=1}^M X^{(m)} \rightarrow E[X] = \int X p(X)dX\]

Example

Suppose that $X_1,X_2, \cdots, X_n \sim N(\mu,\sigma^2)$, where both parameters are unknown. The prior information is given by

\[\begin{aligned}\mu\vert \sigma^2 \sim& N(\mu_0, \frac{\sigma^2}{k})\\\sigma^2 \sim& \text{Inv-Gamma}(\alpha,\beta)\end{aligned}\]

where $k$ is a constant. Provide a Gibbs algorithm to compute $E[g(\mu,\sigma^2)\vert X]$, where $g$ is a function.

The joint distribution is as follows:

\[\begin{aligned}p(\mu, \sigma^2\vert X) \propto &\prod_{i=1}^n f(x_i\vert \mu,\sigma^2)p(\mu\vert \sigma^2)p(\sigma^2)\\=&\left ( \frac{1}{\sqrt{2\pi\sigma^2}}\right ) ^n \exp{\left [ -\frac{\sum_{i=1}^n (x_i-\mu)^2}{2\sigma^2} \right ] } \cdot \left ( \frac{1}{\sqrt{2\pi\frac{\sigma^2}{k}}} \right ) \exp{\left [ -\frac{(\mu-\mu_0)^2}{2\pi\frac{\sigma^2}{k}} \right ] } \cdot \frac{\beta^{\alpha}}{\Gamma(\alpha)} (\sigma^2)^{-(\alpha+1)} \exp{\left [ -\frac{\beta}{\sigma^2} \right ] } \\\propto &(\sigma^2)^{-\left ( \frac{n+1}{2} + \alpha + 1 \right )} \exp{\left [ - \frac{1}{\sigma^2} \left ( \frac{\sum_{i=1}^n (x_i-\mu)^2}{2} + \frac{k(\mu-\mu_0)^2}{2} + \beta \right ) \right ]}\end{aligned}\]

Now, we can derive full conditional distributions for each of parameters from the joint distribution described above.

\[\begin{aligned}p(\mu\vert \sigma^2,X) \propto &p(\mu,\sigma^2\vert X)\\\propto &(\sigma^2)^{-\left ( \frac{n+1}{2} + \alpha + 1 \right )} \exp{\left [ - \frac{1}{\sigma^2} \left ( \frac{\sum_{i=1}^n (x_i-\mu)^2}{2} + \frac{k(\mu-\mu_0)^2}{2} + \beta \right ) \right ]}\\= &(\sigma^2)^{-\left ( \frac{n+1}{2} + \alpha + 1 \right )} \exp{\left [ - \frac{1}{2\sigma^2} \left ( \sum_{i=1}^n (x_i^2-2x_i\mu+\mu^2)+k(\mu^2-2\mu_0\mu+\mu_0^2)+2\beta \right ) \right ]}\\= &(\sigma^2)^{-\left ( \frac{n+1}{2} + \alpha + 1 \right )} \exp{\left [ - \frac{1}{2\sigma^2} \left ( \sum_{i=1}^n x_i^2-2n\bar{x}\mu+n\mu^2 + k\mu^2-2k\mu_0\mu+k\mu_0^2+2\beta \right ) \right ]}\\= &(\sigma^2)^{-\left ( \frac{n+1}{2} + \alpha + 1 \right )} \exp{\left [ - \frac{1}{2\sigma^2} \left ( (n+k)\textcolor{red}{\mu^2}-2(n\bar{x}+k\mu_0)\textcolor{red}{\mu}+\sum_{i=1}^n x_i^2+k\mu_0^2+2\beta \right ) \right ]}\\= &(\sigma^2)^{-\left ( \frac{n+1}{2} + \alpha + 1 \right )} \exp{\left [ - \frac{1}{\frac{2\sigma^2}{n+k}} \left ( \left ( \mu - \frac{n\bar{x}+k\mu_0}{n+k} \right )^2 - \left ( \frac{n\bar{x}+k\mu_0}{n+k} \right )^2 + \frac{\sum_{i=1}^n x_i^2+k\mu_0^2+2\beta}{n+k} \right ) \right ]}\\\propto &\exp{\left [ - \frac{1}{\frac{2\sigma^2}{n+k}} \left ( \mu - \frac{n\bar{x}+k\mu_0}{n+k} \right )^2 \right ]}\\\sim &N\left ( \frac{n\bar{x}+k\mu_0}{n+k}, \frac{\sigma^2}{n+k} \right )\end{aligned}\] \[\begin{aligned}p(\sigma^2\vert \mu,X) \propto &p(\mu,\sigma^2\vert X)\\\propto &(\sigma^2)^{-\left ( \frac{n+1}{2} + \alpha + 1 \right )} \exp{\left [ - \frac{1}{\sigma^2} \left ( \frac{\sum_{i=1}^n (x_i-\mu)^2}{2} + \frac{k(\mu-\mu_0)^2}{2} + \beta \right ) \right ]}\\\sim & \text{Inv-Gamma}\left ( \frac{n+1}{2} + \alpha, \frac{\sum_{i=1}^n (x_i-\mu)^2 + k(\mu-\mu_0)^2}{2} + \beta \right )\end{aligned}\]

Then, we set $\mu^{(0)}$,${\sigma^2}^{(0)}$ as initial values and draw samples from the two full conditional distributions.

\[\begin{aligned}\mu^{(i)}\vert {\sigma^2}^{(i-1)},X \sim &N\left ( \frac{n\bar{x}+k\mu_0}{n+k}, \frac{ {\sigma^2}^{(i-1)} }{n+k} \right )\\{\sigma^2}^{(i)}\vert \mu^{(i)},X \sim &\text{Inv-Gamma}\left ( \frac{n+1}{2} + \alpha, \frac{\sum_{j=1}^n (x_j-\mu^{(i)})^2 + k(\mu^{(i)}-\mu_0)^2}{2} + \beta \right )\end{aligned}\]

After the sufficient number($M$) of iterations, we can get samples for each of parameters:

\[(\mu^{(1)},{\sigma^2}^{(1)}), (\mu^{(2)},{\sigma^2}^{(2)}), \cdots, (\mu^{(M)},{\sigma^2}^{(M)})\]

In practice, it is necessarily needed to perform the burn-in and the auto-correlation function (ACF) test steps. In this example, we assume that we have performed the two steps and the burn-in point is at $5000$th iteration and there is no auto-correlation and $M = 10000$. Based on this assumption, we can calculate the values:

\[g(\mu^{(5001)},{\sigma^2}^{(5001)}), g(\mu^{(5002)},{\sigma^2}^{(5002)}), \cdots, g(\mu^{(10000)},{\sigma^2}^{(10000)})\]

Finally, we can estimate the value of $E[g(\mu,\sigma^2)\vert X]$

\[\frac{1}{5000}\sum_{i=5001}^{10000} g(\mu^{(i)},{\sigma^2}^{(i)}) \rightarrow E[g(\mu,\sigma^2)\vert X]\]

Summary

Comparing the MC method and the MCMC, the purpose of both algorithms is to obtain a sequence of parameter values ${ \theta^{(1)}, \theta^{(2)}, \cdots, \theta^{(M)} }$ such that

\[\frac{1}{M}\sum_{m=1}^M f(\theta^{(m)}) \approx E[f(\theta)\vert X]\]

for any functions $f$ of interest.

However, there exist some differences in their methodology. The MC simulation generates independent samples from a target distribution, whereas the MCMC simulation generates dependent samples from the full conditional distributions. So, we need to check auto-correlation over samples. And, the Gibbs sampling plays important roles in the MCMC method.

References

  1. Walsh - 2004 - Markov chain monte carlo and gibbs sampling
  2. Andrieu et al. - 2003 - An introduction to MCMC for machine learning

See Also