Conjugate Prior

Binomial Distribution

이항 분포는 Bernoulli 시행을 $n$번 독립적으로 반복했을 때의 random variable $X$가 따르는 분포이다. 다시 말하면, true(1)/false(0)의 두 가지 상태로 표현할 수 있는 사건(binary variable)에 대해 여러 시행을 거쳐 특정 observation(관측 결과)이 발생할 확률을 구할 때 사용된다.

\[X \sim B(n,p)\] \[P(X=x)= \binom{n}{x}p^x\left ( 1-p \right )^{n-x}, x=0,1,2,\dots,n\]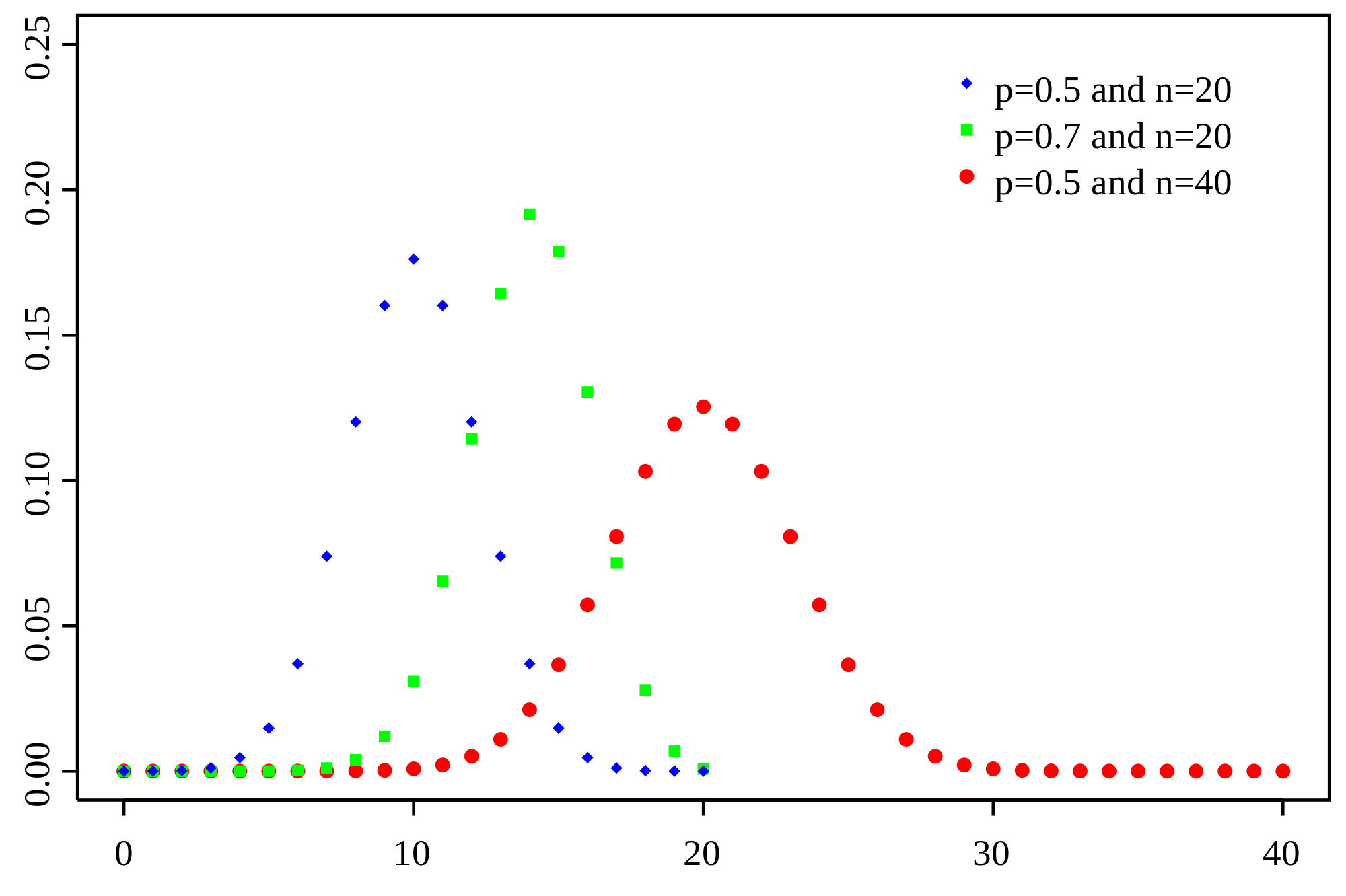

Conjugate Prior

주어진 데이터(observation $X$)가 형성하는 분포의 파라미터($\theta$)를 추정할 때 posterior probability $p(\theta|X)$를 구한다. 베이즈 정리(Bayes’ rule)에서는 likelihood $p(X|\theta)$와 prior $p(\theta)$로 posterior를 구해내는데, 미리 posterior가 어떤 분포를 따르는지 알고 있다면 문제 해결은 상대적으로 간편해진다.

\[p(\theta|X) = \frac{p(X|\theta)p(\theta)}{p(X)}\]

여기서, 특정 분포를 따르는 likelihood에 대해서 posterior가 prior와 동일한 분포를 따르면 posterior probability를 쉽게 계산할 수 있다. 이러한 prior를 likelihood의 conjugate prior라고 한다. 즉, 문제를 해결하는 과정에서 likelihood의 conjugate prior를 취함으로써 posterior의 분포도 알 수 있고(prior의 분포와 같으므로), 계산도 쉬워지는 것이다.

Likelihood $p(X|\theta)$	Conjugate prior $p_0(\theta)$	Posterior $p(\theta|X)$
$Normal(\mu, \sigma)$	$Normal(\mu_0, \sigma_0)$	$Normal(\mu_1, \sigma_1)$
$Binomial(n,p)$	$Beta(\alpha, \beta)$	$Beta(\alpha+n, \beta+N-n)$
$Poisson(\lambda)$	$Gamma(\alpha, \beta)$	$Gamma(\alpha+n, \beta+1)$
$Multinomial(p_1,\dots,p_k)$	$Dirichlet(\alpha_1,\dots,\alpha_k)$	$Dirichlet(\alpha_1+n_1, \dots, \alpha_k+n_k)$

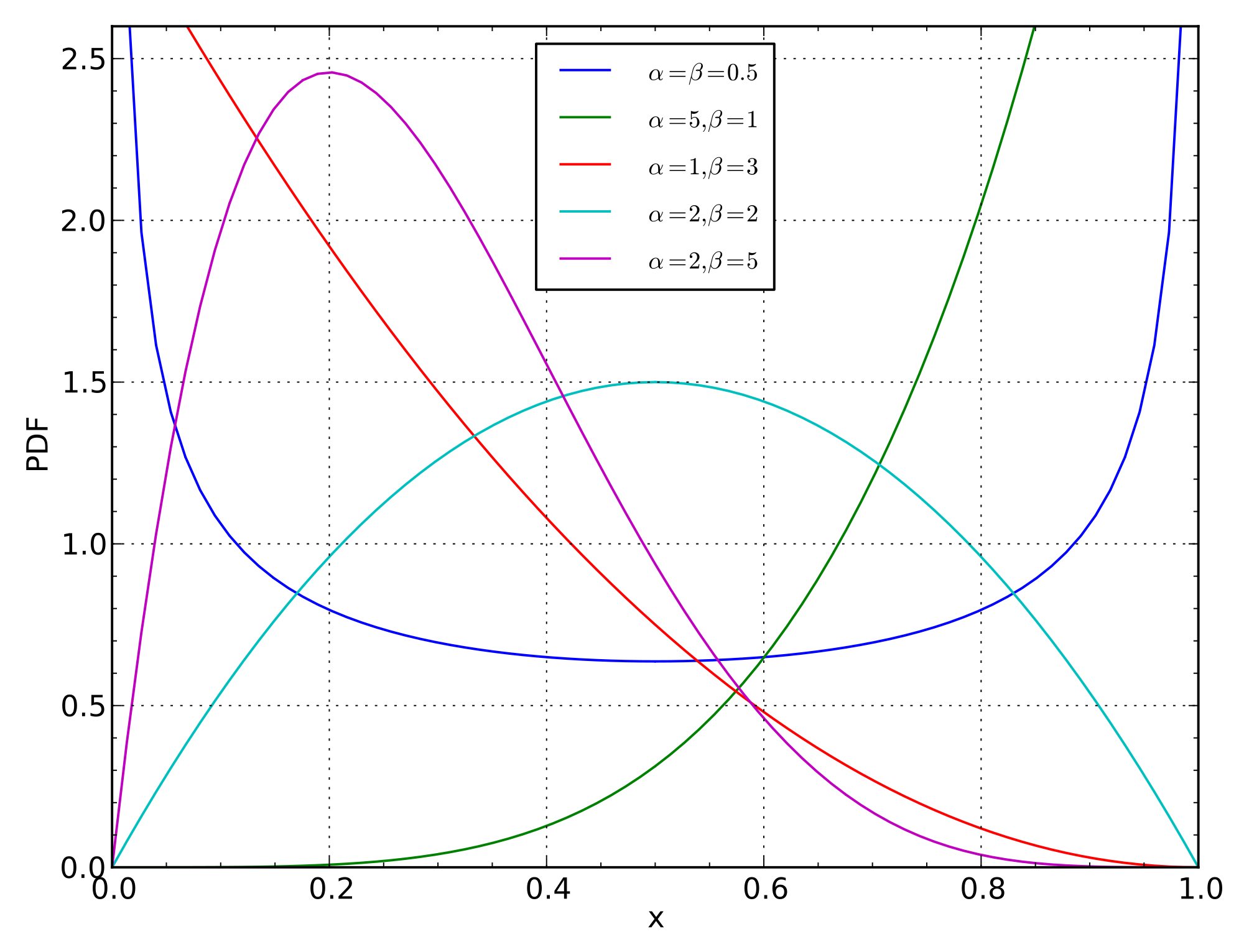
Beta Distribution

베타 분포는 이산 분포(discrete)인 이항 분포와는 다르게 연속 분포(continuous)이다. (참고로 이 속성은 데이터 공학에서 smoothing에 이용되곤 한다.)

Likelihood가 binomial distribution을 따를 때 likelihood의 conjugate prior가 바로 beta distribution이다. 즉, beta distribution에 binomial distribution을 결합하면 다시 beta distribution이 나온다는 것이다.

\[X \sim Beta(\alpha,\beta)\] \[\begin{aligned} f(x) &= \frac{1}{B(\alpha,\beta)}x^{\alpha - 1} (1-x)^{\beta - 1}, &0 \leq x \leq 1\\B(\alpha,\beta)&= \int_0^1 x^{\alpha -1}(1-x)^{\beta-1}dx = \frac{\Gamma(\alpha)\Gamma(\beta)}{\Gamma(\alpha + \beta)}& \end{aligned}\]