Singular Value Decomposition, SVD
Singular Value Decomposition, SVD
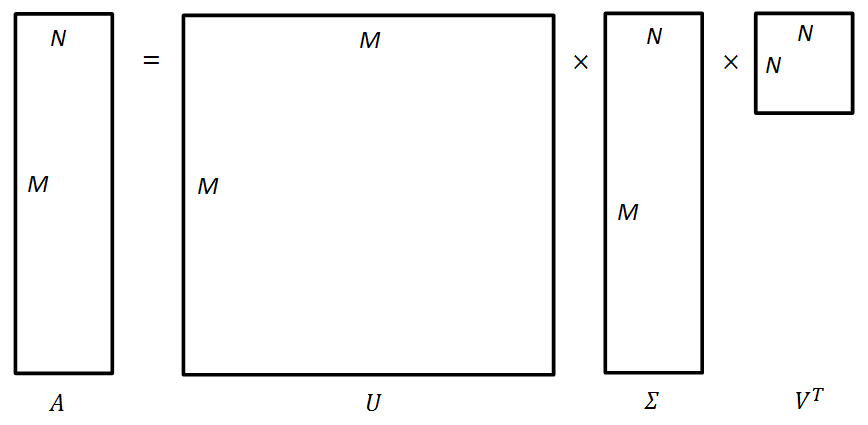
In linear algebra, the singular value decomposition (SVD) is a factorization of a real or complex matrix. Formally, the singular value decomposition of an $M \times N$ real or complex matrix $A$ is a factorization of the form
\[A_{(M\times N)} = U_{(M \times M)}\Sigma_{(M \times N)} V^T_{(N \times N)}\]where $U$ is a $M \times M$ real or complex unitary matrix, $\Sigma$ is a $M \times N$ rectangular diagonal matrix with non-negative real numbers on the diagonal, and $V^T$ (the conjugate transpose of $V$) is a $N \times N$ real or complex unitary matrix. The diagonal entries $\Sigma_{i,j}$ are known as the singular values of $A$.
Intuition
- Rotation with $U$
- Scaling with $\Sigma$
- Rotation with $V^T$
Calculation
Sequence of computing: $A^TA \rightarrow \Sigma \rightarrow V^T \rightarrow U$
- Compute $A^T$ and $A^TA$.
- Determine the eigenvalues of the matrix $A^TA$ and sort these in descending order, in the absolute sense. Square roots these to obtain the singular values of $A$.
- Construct diagonal matrix $\Sigma$ by placing singular values in descending order along its diagonal. Compute its inverse, $\Sigma^{-1}$.
- Use the ordered eigenvalues from Step #2 and compute the eigenvectors of $A^TA$. Place these eigenvectors along the columns of $V$ and compute its transpose, $V^T$.
- Compute $U$ as $U = AV\Sigma^{-1}$. To compute the proof, compute the full $\Sigma VD$ using $A = U\Sigma V^T$.
Low-Rank Approximation
In mathematics, low-rank approximation is a minimization problem which is used for mathematical modeling and data compression.
A best $k$-rank approximation, $\hat{A}_{r=k}$ is given by zeroing out the $r-k$ trailing singular values of $A$, that is
\[\begin{aligned}\hat{A}_{k}=U\hat{\Sigma}_{k}V^T,&&\hat{\Sigma}_{k} = \textbf{diag}(\sigma_1, \cdots, \sigma_k, 0, \cdots, 0)\end{aligned}\]Example
\[A=\begin{pmatrix}1& 0& 0& 0& 2\\0& 0& 3& 0& 0\\ 0& 0& 0& 0& 0\\ 0& 4& 0& 0& 0\end{pmatrix}\]The SVD is given by $A = U\Sigma V^T$, with
\[A = \begin{pmatrix}0& 0& 1& 0\\ 0& 1& 0& 0\\ 0& 0& 0& -1\\ 1& 0& 0& 0\end{pmatrix} \times \begin{pmatrix}4& 0& 0& 0& 0\\0& 3& 0& 0& 0\\ 0& 0& \sqrt{5}& 0& 0\\ 0& 0& 0& 0& 0\end{pmatrix} \times \begin{pmatrix}0& 1& 0& 0& 0\\0& 0& 1& 0& 0\\ \sqrt{0.2}& 0& 0& 0& \sqrt{0.8}\\ 0& 0& 0& 1& 0\\ -\sqrt{0.8}& 0& 0& 0& \sqrt{0.2}\end{pmatrix}\]This matrix is rank $r = 3$. The rank-two approximation is given by zeroing out the smallest singular value, which produces
\[\begin{aligned}\hat{A}_{r=2} &= \begin{pmatrix}0& 0& 1& 0\\ 0& 1& 0& 0\\ 0& 0& 0& -1\\ 1& 0& 0& 0\end{pmatrix} \times \begin{pmatrix}4& 0& 0& 0& 0\\0& 3& 0& 0& 0\\ 0& 0& {\textcolor{Red} 0}& 0& 0\\ 0& 0& 0& 0& 0\end{pmatrix} \times \begin{pmatrix}0& 1& 0& 0& 0\\0& 0& 1& 0& 0\\ \sqrt{0.2}& 0& 0& 0& \sqrt{0.8}\\ 0& 0& 0& 1& 0\\ -\sqrt{0.8}& 0& 0& 0& \sqrt{0.2}\end{pmatrix}\\ &= \begin{pmatrix} 0& 0\\ 0& 1\\ 0& 0\\ 1& 0\end{pmatrix} \times \begin{pmatrix}4& 0\\ 0& 3\end{pmatrix} \times \begin{pmatrix}0& 1& 0& 0& 0\\0& 0& 1& 0& 0\end{pmatrix}\\ &= \begin{pmatrix}0& 0& 0& 0& 0\\0& 0& 3& 0& 0\\ 0& 0& 0& 0& 0\\ 0& 4& 0& 0& 0\end{pmatrix}\end{aligned}\]