Probabilistic Latent Semantic Analysis, PLSA
Topic model
문서들의 집합에서 topic들을 찾아내기 위한 모델로, 눈에 보이는 observation, 즉, given data에 대해 통계적인 방법을 사용하여 모델을 생성하고, 새로운 데이터에 대해서 해당 모델을 적용시켜 원하는 문제를 해결한다.

위에 그림에서 power라는 단어는 정치 토픽으로 쓰여 “국력”을 나타내는 것을 확인할 수 있다. 하지만 power라는 단어만 떼어 놓고 봤을 때, 사람과 관련해서 체력, 지구력 등을 나타낼 때 쓰일 수 있고, 과학에서는 중력, 구심력을 나타내는 표현에 쓰일 수 있고, 수학에서는 지수승을 의미하는 단어로 쓰일 수 있을 것이다. 이렇게 토픽 모델은 문서 내에 특정 단어가 어떤 의미로 쓰였는지 구분해주는 모델이다.
토픽 모델을 사용하면 문서의 내용을 간결하게 나타낼 수 있고, 단어 및 문서 간의 유사도도 평가 가능하다. 그리고 문서 데이터에만 국한되는 것이 아니라 여러 분야에 쓰일 수 있는데, 정보 검색(IR), 인공 지능(AI), 바이오 인포메틱스 등에 다양하게 응용될 수 있다.
Probabilistic Latent Semantic Analysis
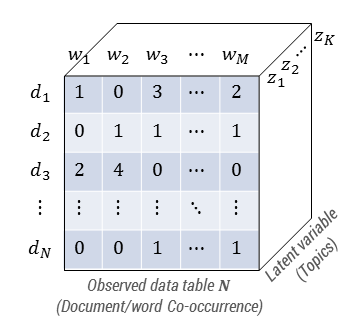
PLSA에서는 observation에 영향을 끼치는 latent variable (topic)의 존재를 가정한다. 그리고 아래 그림과 같이 문서-단어 쌍 $(d,w)$을 observation으로 보고 observation의 생성 확률 $p(d,w)$을 구하고자 한다.
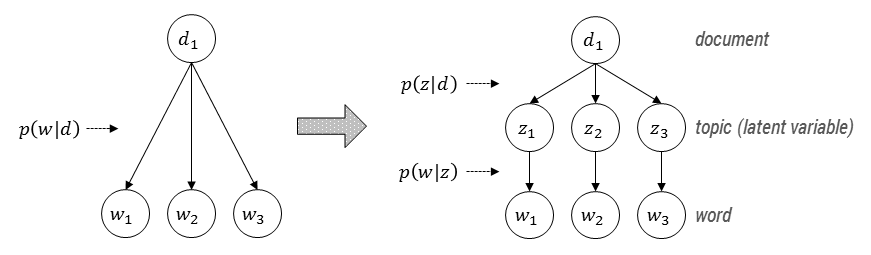
PLSA 모델에서, asymmetric model로 설명하자면, 문서가 주어지고, 문서마다 다양한 topic을 다룰 수 있으며, 그 토픽에 따라 사용될 단어들이 결정된다. (하나의 문서 내에서 각 단어들은 하나의 topic하고만 연관되어 있음) 다시 말하면, 각 문서들은 여러 topic들의 mixture로 나타나고 $p(z \vert d)$는 topic들의 mixing weight로서의 역할을 한다. 이 확률값들은 어디까지나 observation, 즉, $n(d,w)$에 의해 영향을 받게 될 것이다.
Model Fitting with EM Algorithm
EM 알고리즘을 통한 model fitting 과정을 알아보자. 우리의 최종 목표는 주어진 데이터 (observation)에 맞는 모델을 생성하는 것, 즉, observation을 제일 잘 나타내는 확률 분포를 찾는 것인데, 주어진 데이터는 multinomial distribution을 따른다고 가정한다:
\[p(d,w \vert \Theta) = \frac{(\sum_{i,j} n(d_i,w_j))!}{n(d_1,w_1)! \dots n(d_N,w_M)!} p(d_1,w_1)^{n(d_1,w_1)} \dots p(d_N,w_M)^{n(d_N,w_M)}\]Multinomial distribution에서의 parameter $\Theta$는 ${p(d_1,w_1) , \dots, p(d_N,w_M)}$이다. 그런데 PLSA모델에서는 latent variable인 topic $z$의 존재를 가정하고 observation과 topic 간의 확률적 연결을 정의하였기 때문에 다음과 같이 두 가지 버전으로 다시 쓸 수 있다:
\[\begin{aligned}p(d,w)&=p(d)\sum_z p(w \vert z)p(z \vert d)&&\text{(Asymmetric version)}\\&=\sum_z p(z)p(d \vert z)p(w \vert z)&&\text{(Symmetric version)}\end{aligned}\]그리고나서 Expectation-Maximization 과정을 반복 수행하여 이 parameter의 수렴값을 구해내는 것이다. Expectation-Maxization 과정은 다음과 같다:
Expectation
\[p(z \vert d,w) = \frac{p(z)p(d \vert z)p(w \vert z)}{\sum_{z'}p(z')p(d \vert z')p(w \vert z')}\]Maximization
\[\begin{aligned}p(w \vert z) &= \frac{\sum_d n(d,w)p(z \vert d,w)}{\sum_{d,w'}n(d,w')p(z \vert d,w')}\\p(d \vert z)&=\frac{\sum_w n(d,w)p(z \vert d,w)}{\sum_{d',w}n(d',w)p(z \vert d',w)}\\p(z)&=\frac{1}{R}\sum_{d,w}n(d,w)p(z \vert d,w),&R\equiv\sum_{d,w}n(d,w)\end{aligned}\]
Weak Points
PLSA에서 문서 $d$는 $p(z \vert d)$를 mixing weight로 하는 topic $z$의 mixture로 나타나는데, 문서셋 전체에 걸쳐 나타나는 topic distribution $p(z \vert d)$의 경향까지는 나타내지 못한다. 다시 말하면, 모든 문서들은 uniformly 생성된다는 것이다. (There is no generative probabilistic model for the mixing proportions for topics.) 이게 문제가 되는 이유는, 전반적인 토픽의 분포 경향을 분포함수 등으로 나타내지 못하기 때문에 각각의 topic distribution에 대한 정보를 discrete하게 모두 가지고 있어야 한다는 것이다. 그러므로 PLSA의 모델 parameter 수는 주어지는 데이터(training set)의 크기에 linear하게 증가하게 되고($kN+kM$개), 이는 모델이 주어진 데이터에 지나치게 맞춰지는 overfitting의 문제에 이르게 된다. Overfitting이 왜 문제가 되느냐하면 생성된 model이 training data에 너무 맞춰져서 새로운 데이터에 모델을 적용할 수 없다는 것이다. 아래 curve fitting의 예로 overfitting이 왜 안 좋은 지 살펴보자.
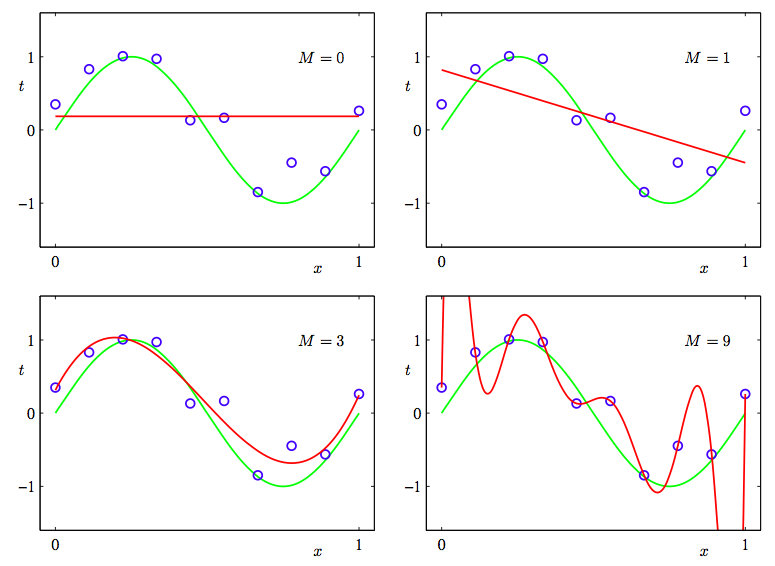
우리가 원하는 이상적인 모델은 green line이다. 하지만 주어진 데이터에 지나치게 맞춰지는 overfitting이 발생하면 모델이 마지막 네 번째 그림에서의 red line처럼 나타날 수 있다. ($M$은 red line의 차수로서, 토픽 모델의 파라미터의 개수에 대응되는 개념이다.) 이렇게 되면 새로운 데이터에 그 모델을 적용할 수 없게 되는 문제가 발생하는 것이다. PLSA 모델은 overfitting에 매우 취약하다. 그래서 본 논문에서는 tempering method(simulated annealing의 역전략)를 제안하지만, overfitting은 여전히 발생할 수 있다.[3] 그래서 discrete한 multinomial parameter space에 (continuous) prior distribution을 부여하는 방법이 제안되는데 그게 바로 LDA 모델이다.
Summing Up
- Input: $N×M$ document/word co-occurrence matrix $(d,w)$, # of topics $K$
- Output: parameters $\Theta = { p(d \vert z); p(w \vert z); p(z) }$
References
- Hofmann - 1999 - Probabilistic latent semantic analysis
- Hofmann - 1999 - Probabilistic latent semantic indexing
- Popescul et al. - 2001 - Probabilistic Models for Unified Collaborative and Content-Based Recommendation in Sparse-Data Environments