PageRank

Motivation

Before introducing the basic concept of PageRank, we should first consider why we need web search engines. Due to the huge scale of the web, it is really difficult to find web pages we want. So, we use web search engines, and they optimize our search to find suitable web pages. The web search engines work as follows:

Basic principle of common Web search engines

Elicit search results by matching a query and keywords of web pages

Sort the results with relative importance of web pages

However, there are a few weak points of prior web search engines. Many of the web search engines, for example, Yahoo!, at that time, simply had utilized incoming-link count as a measure of higher quality search results or more important web pages. Since this way method disregards the importance of web pages, this sort of simple citation counting does not correspond to our common sense notion of importance. Moreover, this way can be easily abused through manipulation. Because it is so easy to make an arbitrary web page on the internet. That’s why the PageRank method had been proposed.

Intuition of PageRank

PageRank computes relative importance for every web page and assigns a rank to each web page. Considering the importance of a web page, we can say a web page is important when many other people also say the web page is important. And, the rank is a numeric value which represents the importance of a web page. (The goal of PageRank is to calculate out the ranks of every web page which exist on the Internet.)

PageRank agrees that a highly linked web page tends to be more “important” than web pages with few incoming-links. In addition to this, PageRank says that a web page is truly important when it is linked by important web pages frequently.

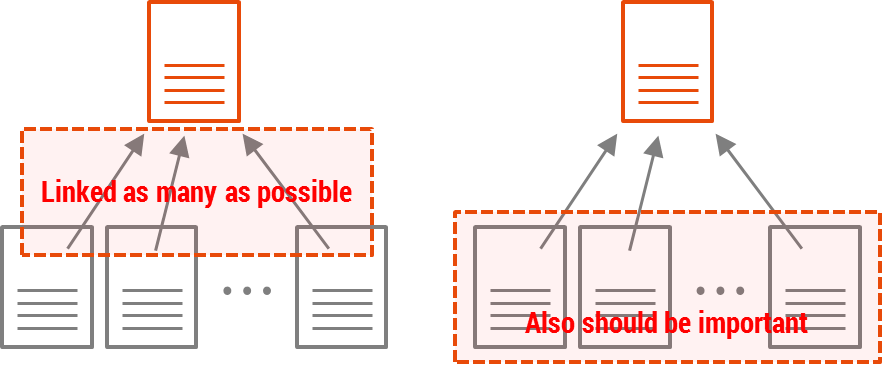
Important page

Web Graph

In order to find ranks of web pages, PageRank utilizes the link structure of the web, where web pages are linked each other by hyperlinks. If we build a graph model to represent the link structure of the web, we can make it easier to understand and solve a problem by using properties of a graph model.

In the web graph model, a web page corresponds to a vertex, and a hyperlink corresponds to an edge:

Hyperlink

With respect to the hyperlink $e$, we can say that web page $u$ references web page $v$. In terms of web page $u$, the hyperlink $e$ is a forward link. On the other hand, in terms of web page $v$, the hyperlink $e$ is a backlink.

Simplified PageRank

Now, let’s figure out how the PageRank algorithm works. In PageRank, the rank propagates from a web page to other pages through hyperlinks. In fact, a hyperlink pointing to a web page can be interpreted as having trust in the contents of the web page. So, how does the rank propagate through hyperlinks?

The rank propagates in the way as follows:

\[R(u) = \sum_{v \in B_u} \frac{R(v)}{N_v}\]

$R(u)$: the rank of web page $u$
$B_u$: the set of web pages which reference web page $u$
$F_v$: the set of web pages which the web page $v$ references
$N_v$: the number of forward links of web page $v$

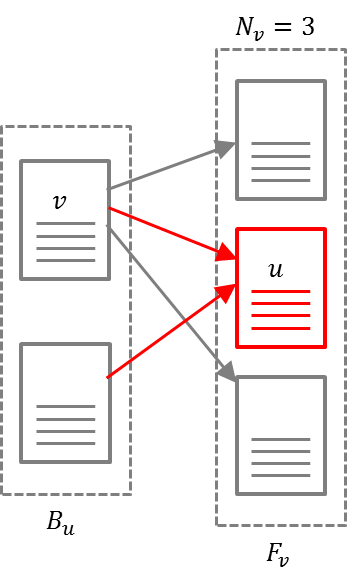
Backlinks of the page 'u'

The rank of a web page is determined by the sum of all received ranks from its backlinks. And the rank is distributed evenly by the number of its forward links.

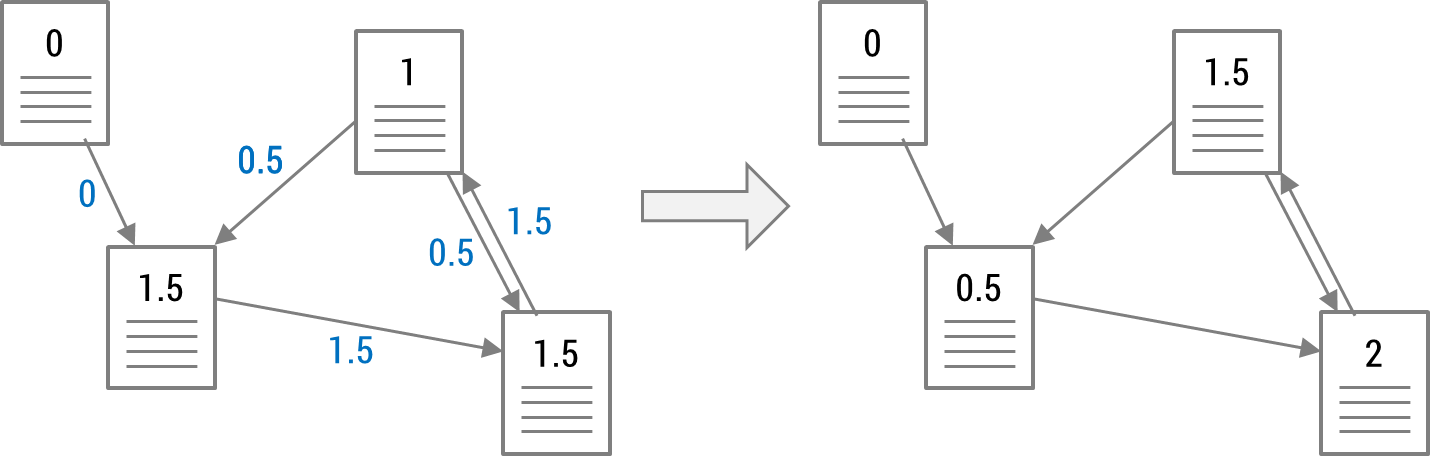
Rank propagation

Such rank propagation performs iteratively. This is to consider not only the influences from web pages located nearby but also the influences of web pages located far away.

So far, we verified how the rank of a web page is calculated. Now, we can represent the rank calculations overall web graph by using the matrix notation.

\[R_{i+1}=S^TR_i\]

$R_i$: a rank vector at $i$-th iteration
$S$: the transition kernel where the sum of entries in a row is $1$

For your reference, the reason why the transposed stochastic matrix is used, is to adjust the direction of process that the rank of a web page, which is determined by the sum of given ranks from backlinks.

Problems with Simplified PageRank

Dangling Links Problem

Dangling nodes cannot deliver their ranks to other web pages. A dangling node is a web page with no forward link, and a dangling link is a hyperlink pointing to dangling nodes. Therefore, dangling nodes keep losing their ranks and thus the sum of ranks in the overall system keep decreasing.

However, dangling links problem can be easily solved by adding virtual links from dangling nodes to all web pages.

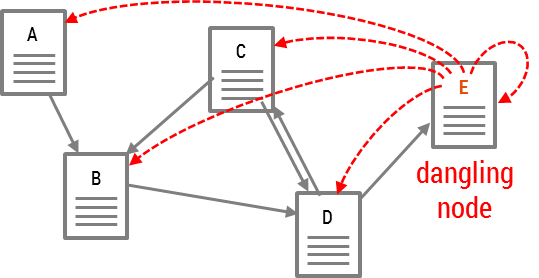
Dangling node

The virtual links enable dangling nodes to deliver their ranks to other web pages. The simplified PageRank formula is modified as follows:

\[R_{i+1}=(S^T+\textbf{w}\times \textbf{d}^T)R_i\]

Vector $\textbf{w}$ represents virtual links, and vector $\textbf{d}$ represents existence of dangling nodes. So, the transition kernel is modified to this looking:

Random jump

RankSink Problem

Another problem is the RankSink Problem. This occurs when some web page references to one of web pages that form a loop.

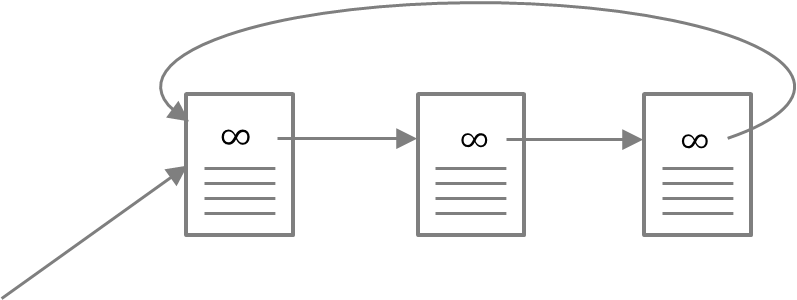
Rank sink problem

This loop will accumulate ranks during iteration but never distribute any rank. So, the web pages in a loop become extremely important. On the other hand, the sum of rank outside the loop relatively keep decreasing.

The RankSink problem is also solved by adding virtual links to all web pages.

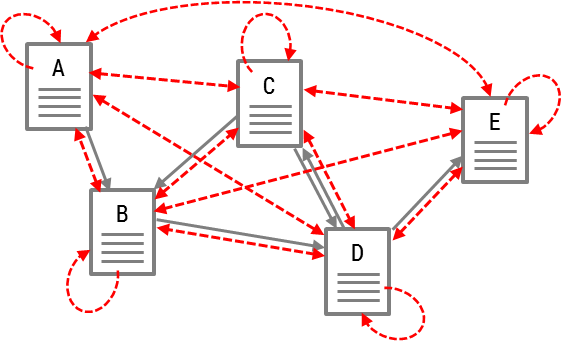
Actual links and virtual links in the web

This way, the web pages in a loop can deliver their ranks to outside the loop through the virtual links. So, the modified PageRank formula is modified once more like this:

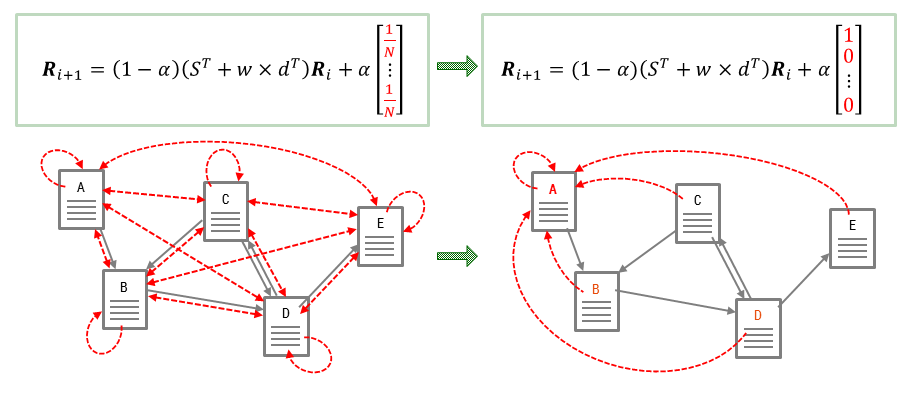
\[R_{i+1}=(1-\alpha)(S^T+\textbf{w}\times \textbf{d}^T)R_i+\alpha \textbf{w}\]

The scalar $\alpha$ is the probability of moving to random web pages, and the vector $\textbf{w}$ represents virtual links.

Random Surfer Model

So far, we have drawn the complete formula of PageRank. In fact, the definition of PageRank has another intuitive basis in random walks on graphs. PageRank is based on intuitive behaviors of a real web surfer. A real web surfer can simply keep clicking on successive links at random and also jump to other web pages through bookmarks or by typing URL. These are named Random walk and Random jump respectively. (This is also called Random Walk with Restart, RWR.)

Termination of Computation

PageRank computation terminates when it converges. Convergence means that the value of $||R_{i+1}-R_i||_1$ gets close to zero. So, we may wonder if the PageRank calculation always converges. The prerequisite for convergence of iterative calculation is that the stochastic matrix of PageRank should have all positive entries. (This is called “regular”.) It is defined in Markov chain:

Markov Chain

The Markov chain is the general model of a system that changes from state to state.

\[\textbf{x}^{(n+1)}=P\textbf{x}^{(n)}\]

$\textbf{x}^{(n)}$: $n$-th state vector
$P$: stochastic transition matrix

The calculation converges only when the matrix $P$ has all positive entries.

Implementation of PageRank

Note that the $d$ factor increases the rate of convergence and maintains $||R||_1$. An alternative normalization is to multiply $R$ by the appropriate factor. The use of $d$ may have a small impact on the influence of $E$.

Because $A$ is a huge size of sparse matrix, the $L1$-norm of $R_{i+1}$ becomes smaller than the $L1$-norm of the prior vector, $R_i$, after the matrix calculation. So, $d > 0$.

\[\begin{aligned}R_0&\leftarrow S\\\text{loop:}&\\R_{i+1}&\leftarrow AR_i\\d&\leftarrow \|R_i\|_1-\|R_{i+1}\|_1\\R_{i+1}&\leftarrow R_{i+1} + dE\\\delta&\leftarrow \|R_{i+1}-R_i\|_1\\\text{while } \delta > \epsilon \end{aligned}\]

Personalized PageRank

The personalized PageRank is one of applications. It can provide personalized search results. By modifying the PageRank formula a little bit to random jump toward one target, web pages which are closely connected with the target will receive relatively high rank. We can consider this as a concept of recommendation.

The personalized page recommendation is available with the personalized PageRank algorithm.